日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

本小題滿分12分）
如圖，已知橢圓C1的中心在原點O，長軸左、右端點M，N在x軸上，橢圓C2的短軸為MN，且C1，C2的離心率都為e，直線l⊥MN，l與C1交于兩點，與C2交于兩點，這四點按縱坐標從大到小依次為A，B，C，D.

（I）設，求與的比值；
（II）當e變化時，是否存在直線l，使得BO∥AN，并說明理由

(本小題滿分12分)
如圖，已知橢圓C₁的中心在圓點O，長軸左、右端點M、N在x軸上，橢圓C₁的短軸為MN，且C₁，C₂的離心率都為e，直線l⊥MN，l與C₁交于兩點，與C₁交于兩點，這四點按縱坐標從大到小依次為A、B、C、D.

（I）設e=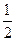，求|BC|與|AD|的比值；
（II）當e變化時，是否存在直線l，使得BO//AN,并說明理由.

 (本小題滿分12分)

如圖，已知橢圓C₁的中心在圓點O，長軸左、右端點M、N在x軸上，橢圓C₁的短軸為MN，且C₁，C₂的離心率都為e，直線l⊥MN，l與C₁交于兩點，與C₁交于兩點，這四點按縱坐標從大到小依次為A、B、C、D.

（I）設e=，求|BC|與|AD|的比值；

（II）當e變化時，是否存在直線l，使得BO//AN,并說明理由.

(本小題滿分12分)

已知向量 a = (cos x,sin x)，b = (－cos x,cos x)，c = (－1,0)

(I)   若 x = ，求向量 a、c 的夾角；

(II)  當 x∈[,] 時，求函數 f (x) = 2a·b + 1 的最大值。

(本小題滿分12分)

已知向量 a = (cos x,sin x)，b = (－cos x,cos x)，c = (－1,0)

(I)   若 x = ，求向量 a、c 的夾角；

(II)  當 x∈[,] 時，求函數 f (x) = 2a·b + 1 的最大值。