日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

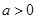（2006年安徽卷）已知函數在R上有定義，對任何實數和任何實數，都有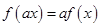

（Ⅰ）證明；

（Ⅱ）證明 其中和均為常數；

（Ⅲ）當（Ⅱ）中的時，設，討論在內的單調性并求極值.

(08年安徽卷理)（本小題滿分12分）

為防止風沙危害，某地決定建設防護綠化帶，種植楊樹、沙柳等植物。某人一次種植了株沙柳。各株沙柳的成活與否是相互獨立的，成活率為，設為成活沙柳的株數，數學期望為3，標準差為。

（Ⅰ）求的值，并寫出的分布列；

（Ⅱ）若有3株或3株以上的沙柳未成活，則需要補種，求需要補種沙柳的概率。

（07年安徽卷理）如圖，和分別是雙曲線的兩個焦點，和是以為圓心，以為半徑的圓與該雙曲線左支的兩個交點，且△是等邊三角形，則雙曲線的離心率為

（A）                （B）            （C）       （D）

（07年安徽卷理）(本小題滿分14分)

設a≥0，f (x)=x－1－ln² x＋2a ln x（x>0）.

（Ⅰ）令F（x）＝xf＇（x），討論F（x）在（0.＋∞）內的單調性并求極值；

（Ⅱ）求證：當x>1時，恒有x>ln²x－2a ln x＋1.

(08年安徽卷理)（本小題滿分12分）

如圖，在四棱錐中，底面是邊長為的菱形，，底面，，為的中點，為的中點．

（I）證明：直線平面．

（II）求異面直線與所成角的大小．

（III）求點到平面的距離．