
題目列表(包括答案和解析)
(本小題滿分12分)現有一張長為40dm,寬為20dm的長方形鐵皮,準備通過分割、焊接成一個無蓋的長方體水箱(損耗忽略不計)。 (1)若從長方形的四個角各截去一個邊長為![]() dm的小正方形,再把四邊向上翻轉
dm的小正方形,再把四邊向上翻轉![]() 角,焊接成一個無蓋的長方體水箱,求:水箱容積的最大值。(2)設(1)中水箱容積的最大值為M,你是否還有其它的設計方案,使你的設計中得到的長方體水箱的容積比M還大?若有,寫出你的設計方案,并求出它的容積;若沒有,請說明理由。
角,焊接成一個無蓋的長方體水箱,求:水箱容積的最大值。(2)設(1)中水箱容積的最大值為M,你是否還有其它的設計方案,使你的設計中得到的長方體水箱的容積比M還大?若有,寫出你的設計方案,并求出它的容積;若沒有,請說明理由。
(本小題滿分12分)已知各項均為正數的數列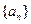 中,
中,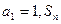 是數列
是數列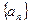 的前
的前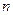 項和,對任意
項和,對任意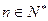 ,有
,有 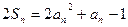 .函數
.函數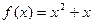 ,數列
,數列 的首項
的首項 .
.
(Ⅰ)求數列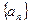 的通項公式;
的通項公式;
(Ⅱ)令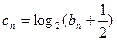 求證:
求證: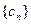 是等比數列并求
是等比數列并求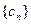 通項公式;
通項公式;
(Ⅲ)令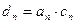 ,
, ,求數列
,求數列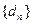 的前n項和
的前n項和 .
.
(本小題滿分12分)
已知各項均為正數的數列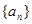 的前n項和
的前n項和 滿足
滿足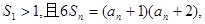
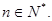
(1)求數列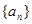 的通項公式;
的通項公式;
(2)設數列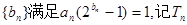 為數列
為數列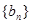 的前n項和,求證:
的前n項和,求證:
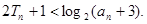
(本小題滿分12分)
已知 是公差為正數的等差數列,首項
是公差為正數的等差數列,首項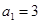 ,前n項和為Sn,數列
,前n項和為Sn,數列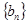 是等比數列,首項
是等比數列,首項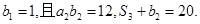
(1)求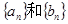 的通項公式.
的通項公式.
(2)令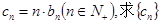 的前n項和Tn.
的前n項和Tn.
(本小題滿分12分)已知各項均為正數的數列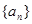 的前
的前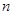 項和
項和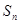 滿足
滿足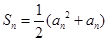
(1)求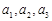 的值; (2)求
的值; (2)求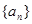 的通項公式;
的通項公式;
(3)是否存在正數 使下列不等式:
使下列不等式:

對一切 成立?若存在,求出M的取值范圍;若不存在,請說明理由
成立?若存在,求出M的取值范圍;若不存在,請說明理由
一、選擇題.(單項選擇,5×12=60分.答案涂在答題卡上的相應位置.)
1.C 2. A 3. B 4. B 5. B 6. B 7. A 8. C 9.D 10. B 11.D 12. B
二、填空題.( 5×4=20分,答案寫在答題紙的相應空格內.)
|