
題目列表(包括答案和解析)
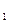 為0.25,在B處的命中率為q
為0.25,在B處的命中率為q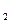 ,該同學選擇先在A處投一球,以后都在B處投,用
,該同學選擇先在A處投一球,以后都在B處投,用 表示該同學投籃訓練結束后所得的總分,其分布列為
表示該同學投籃訓練結束后所得的總分,其分布列為  | 0 | 2 | 3 | 4 | 5 |
| p | 0.03 | P1 | P2 | P3 | P4 |
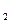 的值;
的值;  的數學期望E
的數學期望E ;
;(本小題滿分12分)(文科做前 兩問;理科全做.)
兩問;理科全做.)
某會議室用3盞燈照明,每盞燈各使用節能燈棍一只,且型號相同.假定每盞燈能否正常照明只與燈棍的壽命有關,該型號的燈棍壽命為1年以上的概率為0.8,壽命為2年以上的概率為0.3,從使 用之日起每滿1年進行一次燈棍更換工作,只更換已壞的燈棍,平時不換.
用之日起每滿1年進行一次燈棍更換工作,只更換已壞的燈棍,平時不換.
(I)在第一次燈棍更換工作中,求不需要更換燈棍的概率;
(I I)在第二次燈棍更換工作中,對其中的某一盞燈來說,求該燈需要更換燈棍的概率;
I)在第二次燈棍更換工作中,對其中的某一盞燈來說,求該燈需要更換燈棍的概率;
(III)設在第二次燈棍更換工作中,需要更換的燈棍數為ξ,求ξ的分布列和期望.
(本小題滿分12分)
已知數列 和
和 滿足:
滿足: ,
, 其中
其中 為實數,
為實數, 為正整數.
為正整數.
(1)對任意實數 ,證明數列
,證明數列 不是等比數列;
不是等比數列;
(2)試判斷數列 是否為等比數列,并證明你的結論;
是否為等比數列,并證明你的結論;
(3)設 ,
, 為數列
為數列 的前
的前 項和.是否存在實數
項和.是否存在實數 ,使得對任意正整數
,使得對任意正整數 ,都有
,都有 ?若存在,求
?若存在,求 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
(本小題滿分12分)已知函數f(x)=x3+x2-2.
(1)設{an}是正數組成的數列,前n項和為Sn,其中a1=3.若點(an,an+12-2an+1)(n∈N*)在函數y=f′(x)的圖象上,求證:點(n,Sn)也在y=f′(x)的圖象上;
(2)求函數f(x)在區間(a-1,a)內的極值.
(本小題滿分12分)某校舉行環保知識大獎賽,比賽分初賽和決賽兩部分,初賽采用選手選一題答一題的方式進行,每位選手最多有 次選題答題的機會,選手累計答對
次選題答題的機會,選手累計答對 題或答錯
題或答錯 題即終止其初賽的比賽:答對
題即終止其初賽的比賽:答對 題者直接進入決賽,答錯
題者直接進入決賽,答錯 題者則被淘汰.已知選手甲答對每個問題的概率相同,并且相互之間沒有影響,答題連續兩次答錯的概率為
題者則被淘汰.已知選手甲答對每個問題的概率相同,并且相互之間沒有影響,答題連續兩次答錯的概率為 .
.
⑴求選手甲可進入決賽的概率;
⑵設選手甲在初賽中答題的個數為 ,試求
,試求 的分布列,并求
的分布列,并求 的數學期望.
的數學期望.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com