
題目列表(包括答案和解析)
(本題滿分14分)
已知函數 ,在點(1,f(1))處的切線方程為y+2=0.
,在點(1,f(1))處的切線方程為y+2=0.
(1) 求函數f(x)的解析式;
(2) 若對于區間[一2,2]上任意兩個自變量的值x1,x2,都有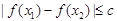 ,求實
,求實
數c的最小值;
(3) 若過點M(2,m)(m≠2),可作曲線y=f(x)的三條切線,求實數m的取值范圍,
(本小題滿分14分)
已知函數f(x)=-![]() x3+bx2+cx+bc,
x3+bx2+cx+bc,
(1)若函數f(x)在x=1處有極值-![]() ,試確定b、c的值;
,試確定b、c的值;
(2)在(1)的條件下,曲線y=f(x)+m與x軸僅有一個交點,求實數m的取值范圍;
(3)記g(x)=|f′( x)|(-1≤x≤1)的最大值為M,若M≥k對任意的b、c恒成立,試求k的取值范圍.
(參考公式:x3-3bx2+4b3=(x+b)(x-2b)2)
 x3+bx2+cx+bc,
x3+bx2+cx+bc,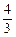 ,試確定b、c的值;
,試確定b、c的值;.(本小題滿分14分)已知函數f (x)=lnx,g(x)=ex.
( I)若函數φ (x) = f (x)-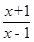 ,求函數φ (x)的單調區間;
,求函數φ (x)的單調區間;
(Ⅱ)設直線l為函數的圖象上一點A(x0,f (x0))處的切線.證明:在區間(1,+∞)上存在唯一的x0,使得直線l與曲線y=g(x)相切.
 ,求函數φ (x)的單調區間;
,求函數φ (x)的單調區間;湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com