
題目列表(包括答案和解析)
 為半圓,AB為半圓直徑,O為半圓圓心,且OD⊥AB,Q為線段OD的中點,已知|AB|=4,曲線C過Q點,動點P在曲線C上運動且保持|PA|+|PB|的值不變.
為半圓,AB為半圓直徑,O為半圓圓心,且OD⊥AB,Q為線段OD的中點,已知|AB|=4,曲線C過Q點,動點P在曲線C上運動且保持|PA|+|PB|的值不變.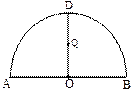
 使
使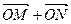 與
與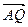 平行,若平行,求出直線
平行,若平行,求出直線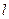 的方程, 若不平行,請說明理由.
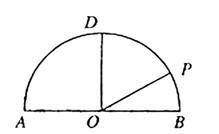
的方程, 若不平行,請說明理由.(本小題滿分12分)如圖,在以點O為圓心,|AB|=4為直徑的半圓ADB中,OD⊥AB,P是半圓弧上一點,∠POB=30°,曲線C是滿足||MA|-|MB||為定值的動點M的軌跡,且曲線C過點P.
(Ⅰ)建立適當的平面直角坐標系,求曲線C的方程;
(Ⅱ)設過點D的直線l與曲線C相交于不同的兩點E、F,求直線l斜率的取值范圍.

(本小題滿分12分)如圖,在以點O為圓心,|AB|=4為直徑的半圓ADB中,OD⊥AB,P是半圓弧上一點,∠POB=30°,曲線C是滿足||MA|-|MB||為定值的動點M的軌跡,且曲線C過點P.
(Ⅰ)建立適當的平面直角坐標系,求曲線C的方程;
(Ⅱ)設過點D的直線l與曲線C相交于不同的兩點E、F,求直線l斜率的取值范圍.
(本題滿分12分)
形狀如圖所示的三個游戲盤中(圖(1)是正方形,M、N分別是所在邊中點,圖(2)是半徑分別為2和4的兩個同心圓,O為圓心,圖(3)是正六邊形,點P為其中心)各有一個玻璃小球,依次搖動三個游戲盤后,將它們水平放置,就完成了一局游戲.
(I)一局游戲后,這三個盤中的小球都停在陰影部分的概率是多少?
(II)用隨機變量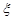 表示一局游戲后,小球停在陰影部分的事件數與小球沒有停在陰影部分的事件數之差的絕對值,求隨機變量
表示一局游戲后,小球停在陰影部分的事件數與小球沒有停在陰影部分的事件數之差的絕對值,求隨機變量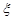 的分布列及數學期望.
的分布列及數學期望.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com