
題目列表(包括答案和解析)
已知Rt△ABC中,![]() ,
,![]() ,有一個圓心角為
,有一個圓心角為![]() ,半徑的長等于
,半徑的長等于![]() 的扇形
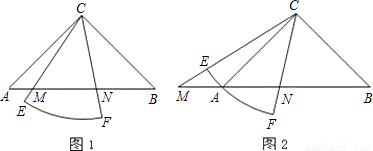
的扇形![]() 繞點C旋轉,且直線CE,CF分別與直線
繞點C旋轉,且直線CE,CF分別與直線![]() 交于點M,N.
交于點M,N.
(Ⅰ)當扇形![]() 繞點C在
繞點C在![]() 的內部旋轉時,如圖①,求證:
的內部旋轉時,如圖①,求證:![]() ;
;
思路點撥:考慮![]() 符合勾股定理的形式,需轉化為在直角三角形中解決.可將△
符合勾股定理的形式,需轉化為在直角三角形中解決.可將△![]() 沿直線
沿直線![]() 對折,得△
對折,得△![]() ,連
,連![]() ,只需證
,只需證![]() ,
,![]() 就可以了.
就可以了.
請你完成證明過程:
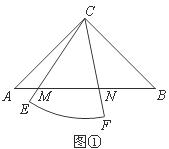
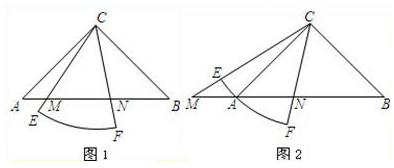
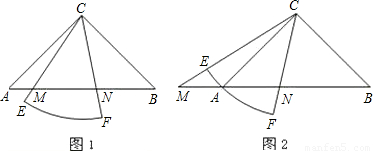
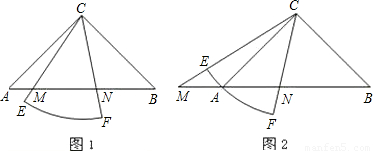
(Ⅱ)當扇形CEF繞點C旋轉至圖②的位置時,關系式![]() 是否仍然成立?若成立,請證明;若不成立,請說明理由.
是否仍然成立?若成立,請證明;若不成立,請說明理由.

一.1.C; 2.C; 3.C; 4.B; 5.D; 6.B; 7.A; 8.B; 9.A; 10.C。
二.11.x≥2; 12.1; 13.25°; 14.145; 15.16;
16.180; 17.①,③; 18..files/image270.gif)
三.19解:原式.files/image272.gif) ?????????????????????????????????????????????????????????????????????????? 2分
?????????????????????????????????????????????????????????????????????????? 2分
.files/image274.gif) ???????????????????????????????????????????????????????????????????????????????????????????? 5分
???????????????????????????????????????????????????????????????????????????????????????????? 5分
當.files/image094.gif) 時,原式
時,原式.files/image277.gif) .??????????????????????????????????????????????????????? 7分.
.??????????????????????????????????????????????????????? 7分.
20.解:(1).files/image279.gif) (名),
(名),
.files/image281.gif) 本次調查了90名學生.?????????????????????????????????????????????????????????????????????????????????????? (2分)
本次調查了90名學生.?????????????????????????????????????????????????????????????????????????????????????? (2分)
補全的條形統計圖如下:
.files/image282.gif) .files/image099.gif) .files/image283.gif) .files/image286.gif) (名), (名),
(3)略(語言表述積極進取,健康向上即可得分).?????????????????????????????????????????????? (7分) 21.(本題滿分8分) 解:(1)如圖,由題意得,∠EAD=45°,∠FBD=30°. ∴ ∠EAC=∠EAD+∠DAC =45°+15°=60°. ∵ AE∥BF∥CD, ∴ ∠FBC=∠EAC=60°. ∴ ∠DBC=30°. ???????????????????????????????????????? 2分 又∵ ∠DBC=∠DAB+∠ADB, ∴ ∠ADB=15°. ∴ ∠DAB=∠ADB. ∴ BD=AB=2. 即B,D之間的距離為 (2)過B作BO⊥DC,交其延長線于點O, 在Rt△DBO中,BD=2,∠DBO=60°. ∴ DO=2×sin60°=2× 在Rt△CBO中,∠CBO=30°,CO=BOtan30°= ∴ CD=DO-CO= 即C,D之間的距離為
(2)290,甲,20.????????????????????????????????????????????????????????????????????????????????? 6分(每空1分) (3)在5月17日,甲廠生產帳篷50頂,乙廠生產帳篷30頂.???????????????????????????????????? 6分 設乙廠每天生產帳篷的數量提高了
答:乙廠每天生產帳篷的數量提高了
23.解:(1)① 等邊三角形;②重疊三角形 (2)用含
(3)能;t=2。.............................................................10分. 24.本小題滿分10分. (Ⅰ)證明 將△ 則△
又由 由
得 又 ∴△ 有 ∴ ∴在Rt△ 得 (Ⅱ)關系式
則△ 有
又由 由
得 又 ∴△ 有 ∴ ∴在Rt△ 得 (3).能;在直線AB上取點M,N使∠MCN=45°......................10分 25.(本題滿分12分) 解:(1)設正方形的邊長為
即 解得
(注:通過觀察、驗證直接寫出正確結果給3分) (2)有側面積最大的情況. 設正方形的邊長為 則
即 改寫為
即當剪去的正方形的邊長為2.25cm時,長方體盒子的側面積最大為40.5cm2.?????????????? 7分
設正方形的邊長為 若按圖1所示的方法剪折,則
即
若按圖2所示的方法剪折,則
即
比較以上兩種剪折方法可以看出,按圖2所示的方法剪折得到的盒子側面積最大,即當剪去的正方形的邊長為 說明:解答題各小題只給了一種解答及評分說明,其他解法只要步驟合理,解答正確,均應給出相應分數. 26.(本小題滿分12分) 解:(1)在Rt△ABC中, 由題意知:AP = 5-t,AQ = 2t, 若PQ∥BC,則△APQ ∽△ABC, ∴ ∴
(2)過點P作PH⊥AC于H. ∵△APH ∽△ABC, ∴ ∴ ∴ ∴ (3)若PQ把△ABC周長平分, 則AP+AQ=BP+BC+CQ. ∴ 解得: 若PQ把△ABC面積平分, 則 ∵ t=1代入上面方程不成立, ∴不存在這一時刻t,使線段PQ把Rt△ACB的周長和面積同時平分.???????????????? 9′ (4)過點P作PM⊥AC于M,PN⊥BC于N,
∵PM⊥AC于M, ∴QM=CM. ∵PN⊥BC于N,易知△PBN∽△ABC. ∴ ∴ ∴ ∴ 解得: ∴當 此時 在Rt△PMC中, ∴菱形PQP ′ C邊長為
同步練習冊答案 湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區 違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。 ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號 |