
題目列表(包括答案和解析)
(本小題滿分8分)
為了了解某市在減輕學生作業負擔的工作上的落實情況,該市教育局對某校某班每個同學晚上完成作業的時間進行了一次調查統計,并根據收集的數據繪制了如圖所示的兩幅不完整的統計圖,請你根據圖中提供的信息,完成下面的問題
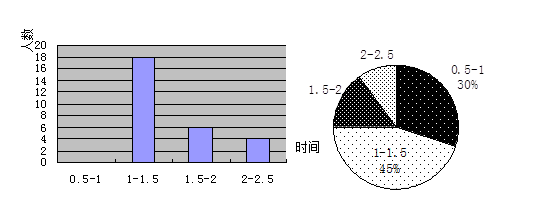
1.(1)該班共有多少學生?
2.(2)將圖中的條形統計圖補充完整
3.(3)求作業完成時間在0.5-1小時的部分對應扇形圓心角是多少度?
4.(4)如果該校七年級共有1000名學生,請估計七年級學生完成作業時間超過1.5小時的大約有多少人?
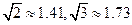 )
) (本小題滿分8分)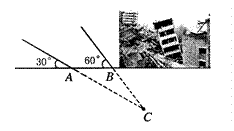
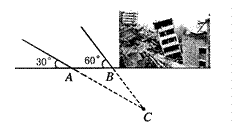
2011年3月10日,云南盈江縣發生里氏5.8級地震。蕭山金利浦地震救援隊接到上級命令后立即趕赴震區進行救援。救援隊利用生命探測儀在某建筑物廢墟下方探測到點 C 處有生命跡象,已知廢墟一側地面上兩探測點A、B 相距3米,探測線與地面的夾角分別是30°和 60°(如圖),試確定生命所在點 C 的深度。(結果精確到0.1米,參考數據: )
)
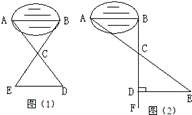
(本小題滿分12分)某班同學到野外活動,為測量一池塘兩端A、B的距離,設計了幾種方案,下面介紹兩種:(I)如圖(1),先在平地取一個可以直接到達A、B的點C,并分別延長AC到D,BC到E,使DC=AC,BC=EC,最后測出DE的距離即為AB的長。(II)如圖(2),先過B點作AB的垂線BF,再在BF上取C、D兩點,使BC=CD,接著過點D作BD的垂線DE,交AC的延長線于E,則測出DE的長即為AB的距離。閱讀后回答下列問題: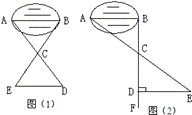
【小題1】(1)方案(I)是否可行?為什么?
【小題2】(2)方案(II)是否切實可行?為什么?
【小題3】(3)方案(II)中作BF⊥AB,ED⊥BF的目的是 ;若僅滿足∠ABD=∠BDE≠90°,方案(II)是否成立?
【小題4】(4)方案(II)中,若使BC=n·CD,能否測得(或求出)AB的長?理由是 ,若ED=m,則AB= 。
一.1.C; 2.C; 3.C; 4.B; 5.D; 6.B; 7.A; 8.B; 9.A; 10.C。
二.11.x≥2; 12.1; 13.25°; 14.145; 15.16;
16.180; 17.①,③; 18..files/image270.gif)
三.19解:原式.files/image272.gif) ?????????????????????????????????????????????????????????????????????????? 2分
?????????????????????????????????????????????????????????????????????????? 2分
.files/image274.gif) ???????????????????????????????????????????????????????????????????????????????????????????? 5分
???????????????????????????????????????????????????????????????????????????????????????????? 5分
當.files/image094.gif) 時,原式
時,原式.files/image277.gif) .??????????????????????????????????????????????????????? 7分.
.??????????????????????????????????????????????????????? 7分.
20.解:(1).files/image279.gif) (名),
(名),
.files/image281.gif) 本次調查了90名學生.?????????????????????????????????????????????????????????????????????????????????????? (2分)
本次調查了90名學生.?????????????????????????????????????????????????????????????????????????????????????? (2分)
補全的條形統計圖如下:
.files/image282.gif) .files/image099.gif) .files/image283.gif) .files/image286.gif) (名), (名),
(3)略(語言表述積極進取,健康向上即可得分).?????????????????????????????????????????????? (7分) 21.(本題滿分8分) 解:(1)如圖,由題意得,∠EAD=45°,∠FBD=30°. ∴ ∠EAC=∠EAD+∠DAC =45°+15°=60°. ∵ AE∥BF∥CD, ∴ ∠FBC=∠EAC=60°. ∴ ∠DBC=30°. ???????????????????????????????????????? 2分 又∵ ∠DBC=∠DAB+∠ADB, ∴ ∠ADB=15°. ∴ ∠DAB=∠ADB. ∴ BD=AB=2. 即B,D之間的距離為 (2)過B作BO⊥DC,交其延長線于點O, 在Rt△DBO中,BD=2,∠DBO=60°. ∴ DO=2×sin60°=2× 在Rt△CBO中,∠CBO=30°,CO=BOtan30°= ∴ CD=DO-CO= 即C,D之間的距離為
(2)290,甲,20.????????????????????????????????????????????????????????????????????????????????? 6分(每空1分) (3)在5月17日,甲廠生產帳篷50頂,乙廠生產帳篷30頂.???????????????????????????????????? 6分 設乙廠每天生產帳篷的數量提高了
答:乙廠每天生產帳篷的數量提高了
23.解:(1)① 等邊三角形;②重疊三角形 (2)用含
(3)能;t=2。.............................................................10分. 24.本小題滿分10分. (Ⅰ)證明 將△ 則△
又由 由
得 又 ∴△ 有 ∴ ∴在Rt△ 得 (Ⅱ)關系式
則△ 有
又由 由
得 又 ∴△ 有 ∴ ∴在Rt△ 得 (3).能;在直線AB上取點M,N使∠MCN=45°......................10分 25.(本題滿分12分) 解:(1)設正方形的邊長為
即 解得
(注:通過觀察、驗證直接寫出正確結果給3分) (2)有側面積最大的情況. 設正方形的邊長為 則
即 改寫為
即當剪去的正方形的邊長為2.25cm時,長方體盒子的側面積最大為40.5cm2.?????????????? 7分
設正方形的邊長為 若按圖1所示的方法剪折,則
即
若按圖2所示的方法剪折,則
即
比較以上兩種剪折方法可以看出,按圖2所示的方法剪折得到的盒子側面積最大,即當剪去的正方形的邊長為 說明:解答題各小題只給了一種解答及評分說明,其他解法只要步驟合理,解答正確,均應給出相應分數. 26.(本小題滿分12分) 解:(1)在Rt△ABC中, 由題意知:AP = 5-t,AQ = 2t, 若PQ∥BC,則△APQ ∽△ABC, ∴ ∴
(2)過點P作PH⊥AC于H. ∵△APH ∽△ABC, ∴ ∴ ∴ ∴ (3)若PQ把△ABC周長平分, 則AP+AQ=BP+BC+CQ. ∴ 解得: 若PQ把△ABC面積平分, 則 ∵ t=1代入上面方程不成立, ∴不存在這一時刻t,使線段PQ把Rt△ACB的周長和面積同時平分.???????????????? 9′ (4)過點P作PM⊥AC于M,PN⊥BC于N,
∵PM⊥AC于M, ∴QM=CM. ∵PN⊥BC于N,易知△PBN∽△ABC. ∴ ∴ ∴ ∴ 解得: ∴當 此時 在Rt△PMC中, ∴菱形PQP ′ C邊長為
同步練習冊答案 湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區 違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。 ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號 |