欧美精品xx,一级大片免费观看,中文字幕日韩专区

高考對二項式定理的考查.以二項式展開式及其通項公式內容為主.要有目標意識和構造意識.要注意展開式的通項公式正.反兩方面的應用.此類題也可分兩類.(1)直接運用通項公式求特定項的系數或與系數有關的問題.(2)需用轉化思想化歸為二項問題來處理的問題. 【查看更多】

學校為測評班級學生對任課教師的滿意度，采用“100分制”打分的方式來計分．現從某班學生中隨機抽取10名，以下莖葉圖記錄了他們對某教師的滿意度分數(以十位數字為莖，個位數字為葉)：

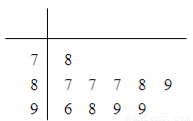
（1）指出這組數據的眾數和中位數；

（2）若滿意度不低于98分，則評價該教師為“優秀”．求從這10人中隨機選取3人，至多有1人評價

該教師是“優秀”的概率；

（3）以這10人的樣本數據來估計整個班級的總體數據，若從該班任選3人，記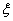表示抽到評價該教師為

“優秀”的人數，求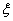的分布列及數學期望．

查看答案和解析>>

已知f（x）=a²x-

1

2

x³，x∈（-2，2）為正常數．
（1）可以證明：定理“若a、b∈R^*，則

a+b

2

≥

ab

（當且僅當a=b時取等號）”推廣到三個正數時結論是正確的，試寫出推廣后的結論（無需證明）；
（2）若f（x）＞0在（0，2）上恒成立，且函數f（x）的最大值大于1，求實數a的取值范圍，并由此猜測y=f（x）的單調性（無需證明）；
（3）對滿足（2）的條件的一個常數a，設x=x₁時，f（x）取得最大值．試構造一個定義在D={x|x＞-2，且x≠4k-2，k∈N}上的函數g（x），使當x∈（-2，2）時，g（x）=f（x），當x∈D時，g（x）取得最大值的自變量的值構成以x₁為首項的等差數列．

查看答案和解析>>

已知f（x）=a²x-

x³，x∈（-2，2）為正常數．
（1）可以證明：定理“若a、b∈R^*，則

（當且僅當a=b時取等號）”推廣到三個正數時結論是正確的，試寫出推廣后的結論（無需證明）；
（2）若f（x）＞0在（0，2）上恒成立，且函數f（x）的最大值大于1，求實數a的取值范圍，并由此猜測y=f（x）的單調性（無需證明）；
（3）對滿足（2）的條件的一個常數a，設x=x₁時，f（x）取得最大值．試構造一個定義在D={x|x＞-2，且x≠4k-2，k∈N}上的函數g（x），使當x∈（-2，2）時，g（x）=f（x），當x∈D時，g（x）取得最大值的自變量的值構成以x₁為首項的等差數列．

查看答案和解析>>

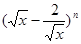已知二項展開式中，第4項的二項式系數與第3項的二項式系數的比為8:3.（I）求n的值；（II）求展開式中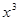項的系數.

【解析】本試題主要是考查了二項式定理的運用，求解通項公式的項的運用。

查看答案和解析>>

已知f（x）=a²x-

1

2

x³，x∈（-2，2）為正常數．
（1）可以證明：定理“若a、b∈R^*，則

a+b

2

≥

ab

（當且僅當a=b時取等號）”推廣到三個正數時結論是正確的，試寫出推廣后的結論（無需證明）；
（2）若f（x）＞0在（0，2）上恒成立，且函數f（x）的最大值大于1，求實數a的取值范圍，并由此猜測y=f（x）的單調性（無需證明）；
（3）對滿足（2）的條件的一個常數a，設x=x₁時，f（x）取得最大值．試構造一個定義在D={x|x＞-2，且x≠4k-2，k∈N}上的函數g（x），使當x∈（-2，2）時，g（x）=f（x），當x∈D時，g（x）取得最大值的自變量的值構成以x₁為首項的等差數列．

查看答案和解析>>

日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

練習冊

高中

初中

小學