
題目列表(包括答案和解析)
(本小題滿分12分)如圖,已知正方體ABCD—A1B1C1D1的棱長為2,E、F分別是A1B1、CC1的中點,過D1、E、F作平面D1EGF交BB1于G。 (1)求證:EG//D1F; (2)求銳二面角C1—D1E—F的余弦值。
(本小題滿分12分)如圖,已知正方形ABCD和矩形ACEF所在平面互相垂直,
AB=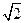 ,AF=1,M是線段EF的中點。
,AF=1,M是線段EF的中點。
(Ⅰ)求證:AM∥平面BDE;
(Ⅱ) 求二面角A-DF-B的大小.
(Ⅲ)試問:在線段AC上是否存在一點P,使得直線PF與AD所成角為60°?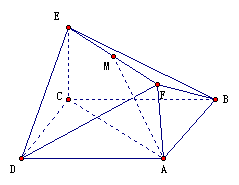
(本小題滿分12分)如圖,已知正方形ABCD和矩形ACEF所在平面互相垂直,
AB=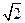 ,AF=1,M是線段EF的中點。
,AF=1,M是線段EF的中點。
(Ⅰ)求證:AM∥平面BDE;
(Ⅱ) 求二面角A-DF-B的大小.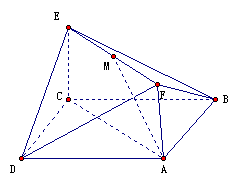
(本小題滿分12分)如圖,已知正三棱柱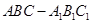 的各棱長都是4,
的各棱長都是4, 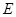 是
是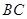 的中點,動點
的中點,動點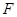 在側棱
在側棱 上,且不與點
上,且不與點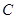 重合.
重合.
(I)當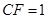 時,求證:
時,求證: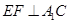 ;
;
(II)設二面角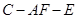 的大小為
的大小為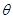 ,求
,求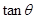 的最小值.
的最小值.
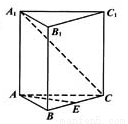
(本小題滿分12分)
如圖,已知正三棱柱ABC—A1B1C1的底面邊長是2,D是CC1的中點,直線AD與側面BB1C1C所成的角是45°.
(I)求二面角A—BD—C的大小;
(II)求點C到平面ABD的距離.

題 號
1
2
3
4
5
6
7
8
9
10
答 案
.files/image350.gif)
.files/image046.gif)
.files/image350.gif)
.files/image044.gif)
.files/image046.gif)
.files/image042.gif)
.files/image042.gif)
.files/image044.gif)
.files/image359.gif)
.files/image042.gif)
11. .files/image362.gif) ;
12.
;
12. .files/image364.gif) ;
13.
;
13..files/image366.gif) 或
或.files/image128.gif) 或
或.files/image369.gif) ; 14.
; 14..files/image371.gif) ; 15.
; 15..files/image373.gif) .
.
三、解答題(本大題共6小題,共75分)
16.(本小題滿分12分)
已知向量.files/image223.gif) ,
,.files/image225.gif) (
(.files/image144.gif) ,
,.files/image228.gif) ).函數
).函數.files/image230.gif) ,
,
.files/image232.gif) 的圖象的一個對稱中心與它相鄰的一條對稱軸之間的距離為
的圖象的一個對稱中心與它相鄰的一條對稱軸之間的距離為.files/image126.gif) ,且過點
,且過點.files/image235.gif) .
.
(Ⅰ)求函數.files/image237.gif) 的表達式;
的表達式;
(Ⅱ)當.files/image239.gif) 時,求函數
時,求函數.files/image237.gif) 的單調區間。
的單調區間。
【解】(Ⅰ).files/image375.gif)
.files/image377.gif) …………3′
…………3′
由題意得周期.files/image379.gif) ,故
,故.files/image381.gif) .…………4′
.…………4′
又圖象過點.files/image235.gif) ,∴
,∴.files/image384.gif)
即.files/image386.gif) ,而
,而.files/image228.gif) ,∴
,∴.files/image389.gif) ,∴
,∴.files/image391.gif) ………6′
………6′
(Ⅱ)當.files/image239.gif) 時,
時,.files/image393.gif)
∴當.files/image395.gif) 時,即
時,即.files/image397.gif) 時,
時,.files/image237.gif) 是減函數
是減函數
當.files/image399.gif) 時,即
時,即.files/image401.gif) 時,
時,.files/image237.gif) 是增函數
是增函數
∴函數.files/image237.gif) 的單調減區間是
的單調減區間是.files/image403.gif) ,單調增區間是
,單調增區間是.files/image405.gif) …………12′
…………12′
17.(本小題滿分12分)
在某社區舉辦的《2008奧運知識有獎問答比賽》中,甲、乙、丙三人同時回答一道有關奧運知識的問題,已知甲回答這道題對的概率是.files/image241.gif) ,甲、丙兩人都回答錯的概率是
,甲、丙兩人都回答錯的概率是.files/image243.gif) ,乙、丙兩人都回答對的概率是
,乙、丙兩人都回答對的概率是.files/image245.gif) .
.
(Ⅰ)求乙、丙兩人各自回答這道題對的概率;
(Ⅱ)用.files/image247.gif) 表示回答該題對的人數,求
表示回答該題對的人數,求.files/image247.gif) 的分布列和數學期望
的分布列和數學期望.files/image249.gif) .
.
【解】(Ⅰ)記“甲回答對這道題”、“ 乙回答對這道題”、“丙回答對這道題”分別為事件.files/image407.gif) 、
、.files/image409.gif) 、
、.files/image411.gif) ,則
,則.files/image413.gif) ,且有
,且有.files/image415.gif) ,即
,即.files/image417.gif)
∴.files/image419.gif) ,
,.files/image421.gif) .…………6′
.…………6′
(Ⅱ)由(Ⅰ).files/image423.gif) ,
,.files/image425.gif) .
.
.files/image247.gif) 的可能取值為:
的可能取值為:.files/image428.gif) 、
、.files/image126.gif) 、
、.files/image431.gif) 、
、.files/image190.gif) .
.
則.files/image433.gif) ;
;
.files/image435.gif) ;
;
.files/image437.gif) ;
;
.files/image439.gif) .…………9′
.…………9′
∴.files/image247.gif) 的分布列為
的分布列為
.files/image247.gif)
.files/image428.gif)
.files/image126.gif)
.files/image431.gif)
.files/image190.gif)
.files/image060.gif)
.files/image446.gif)
.files/image448.gif)
.files/image450.gif)
.files/image452.gif)
.files/image454.gif) 的數學期望
的數學期望.files/image456.gif) .…………12′
.…………12′
18.(本小題滿分12分)如圖,已知正三棱柱.files/image251.gif) 各棱長都為
各棱長都為.files/image209.gif) ,
,.files/image060.gif) 為棱
為棱.files/image255.gif) 上的動點。
上的動點。
(Ⅰ)試確定.files/image257.gif) 的值,使得
的值,使得.files/image259.gif) ;(Ⅱ)若
;(Ⅱ)若.files/image261.gif) ,求二面角
,求二面角.files/image263.gif) 的大小;
的大小;
(Ⅲ)在(Ⅱ)的條件下,求點.files/image265.gif) 到面
到面.files/image267.gif) 的距離。
的距離。
【法一】(Ⅰ)當.files/image259.gif) 時,作
時,作.files/image060.gif) 在
在.files/image207.gif) 上的射影
上的射影.files/image350.gif) . 連結
. 連結.files/image462.gif) .
.
則.files/image464.gif) 平面
平面.files/image466.gif) ,∴
,∴.files/image468.gif) ,∴
,∴.files/image350.gif) 是
是.files/image207.gif) 的中點,又
的中點,又.files/image472.gif) ,∴
,∴.files/image474.gif) 也是
也是.files/image476.gif) 的中點,
的中點,
即.files/image478.gif) . 反之當
. 反之當.files/image478.gif) 時,取
時,取.files/image480.gif) 的中點
的中點.files/image482.gif) ,連接
,連接.files/image484.gif) 、
、.files/image486.gif) .
.
∵.files/image215.gif) 為正三角形,∴
為正三角形,∴.files/image489.gif) . 由于
. 由于.files/image060.gif) 為
為.files/image255.gif) 的中點時,
的中點時,.files/image493.gif)
.files/image495.jpg) ∵
∵.files/image497.gif) 平面
平面.files/image132.gif) ,∴
,∴.files/image500.gif) 平面
平面.files/image132.gif) ,∴
,∴.files/image502.gif) .……4′
.……4′
(Ⅱ)當.files/image261.gif) 時,作
時,作.files/image060.gif) 在
在.files/image207.gif) 上的射影
上的射影.files/image350.gif) . 則
. 則.files/image504.gif) 底面
底面.files/image132.gif) .
.
作.files/image350.gif) 在
在.files/image508.gif) 上的射影
上的射影.files/image510.gif) ,連結
,連結.files/image512.gif) ,則
,則.files/image514.gif) .
.
∴.files/image516.gif) 為二面角
為二面角.files/image263.gif) 的平面角。
的平面角。
又∵.files/image472.gif) ,∴
,∴.files/image518.gif) ,∴
,∴.files/image520.gif) .
.
∴.files/image522.gif) ,又∵
,又∵.files/image524.gif) ,∴
,∴.files/image526.gif) .
.
∴.files/image528.gif) ,∴
,∴.files/image263.gif) 的大小為
的大小為.files/image531.gif) .…8′
.…8′
(Ⅲ)設.files/image265.gif) 到面
到面.files/image267.gif) 的距離為
的距離為.files/image533.gif) ,則
,則.files/image535.gif) ,∵
,∵.files/image472.gif) ,∴
,∴.files/image537.gif) 平面
平面.files/image539.gif) ,
,
∴.files/image541.gif) 即為
即為.files/image060.gif) 點到平面
點到平面.files/image539.gif) 的距離,
的距離,
又.files/image545.gif) ,∴
,∴.files/image547.gif) .
.
.files/image549.jpg) 即
即.files/image551.gif) ,解得
,解得.files/image553.gif) .即
.即.files/image265.gif) 到面
到面.files/image267.gif) 的距離為
的距離為.files/image555.gif) .……12′
.……12′
【法二】以.files/image042.gif) 為原點,
為原點,.files/image207.gif) 為
為.files/image020.gif) 軸,過
軸,過.files/image042.gif) 點與
點與.files/image207.gif) 垂直的直線為
垂直的直線為.files/image177.gif) 軸,
軸,
.files/image561.gif) 為
為.files/image563.gif) 軸,建立空間直角坐標系
軸,建立空間直角坐標系.files/image565.gif) ,如圖所示,
,如圖所示,
設.files/image567.gif) ,則
,則.files/image569.gif) 、
、.files/image571.gif) 、
、.files/image573.gif) .
.
(Ⅰ)由.files/image575.gif) 得
得.files/image577.gif) ,
,
即.files/image579.gif) ,∴
,∴.files/image581.gif) ,即
,即.files/image060.gif) 為
為.files/image255.gif) 的中點,
的中點,
也即.files/image478.gif) 時,
時,.files/image502.gif) .…………4′
.…………4′
(Ⅱ)當.files/image261.gif) 時,
時,.files/image060.gif) 點的坐標是
點的坐標是.files/image586.gif) . 取
. 取.files/image588.gif) .
.
則.files/image590.gif) ,
,.files/image592.gif) .
.
∴.files/image594.gif) 是平面
是平面.files/image267.gif) 的一個法向量。
的一個法向量。
又平面.files/image132.gif) 的一個法向量為
的一個法向量為.files/image598.gif) .
.
∴.files/image600.gif) ,∴二面角
,∴二面角.files/image602.gif) 的大小是
的大小是.files/image604.gif) .……8′
.……8′
(Ⅲ)設.files/image265.gif) 到面
到面.files/image267.gif) 的距離為
的距離為.files/image533.gif) ,則
,則.files/image606.gif) ,∴
,∴.files/image265.gif) 到面
到面.files/image267.gif) 的距離為
的距離為.files/image555.gif) .…12′
.…12′
19.(本小題滿分12分)
已知函數.files/image270.gif) .
.
(Ⅰ)求函數.files/image237.gif) 的單調區間和極值;
的單調區間和極值;
(Ⅱ)若.files/image273.gif) 對滿足
對滿足.files/image275.gif) 的任意實數
的任意實數.files/image020.gif) 恒成立,求實數
恒成立,求實數.files/image064.gif) 的取值范圍(這里
的取值范圍(這里.files/image100.gif) 是自然對數的底數);
是自然對數的底數);
(Ⅲ)求證:對任意正數.files/image209.gif) 、
、.files/image211.gif) 、
、.files/image038.gif) 、
、.files/image283.gif) ,恒有
,恒有.files/image285.gif)
.files/image287.gif) .
.
【解】(Ⅰ).files/image609.gif)
∴.files/image237.gif) 的增區間為
的增區間為.files/image611.gif) ,
,.files/image237.gif) 減區間為
減區間為.files/image613.gif) 和
和.files/image615.gif) .
.
極大值為.files/image617.gif) ,極小值為
,極小值為.files/image619.gif) .…………4′
.…………4′
(Ⅱ)原不等式可化為.files/image621.gif) 由(Ⅰ)知,
由(Ⅰ)知,.files/image275.gif) 時,
時,.files/image624.gif) 的最大值為
的最大值為.files/image626.gif) .
.
∴.files/image628.gif) 的最大值為
的最大值為.files/image630.gif) ,由恒成立的意義知道
,由恒成立的意義知道.files/image632.gif) ,從而
,從而.files/image634.gif) …8′
…8′
(Ⅲ)設.files/image636.gif)
則.files/image638.gif) .
.
∴當.files/image640.gif) 時,
時,.files/image642.gif) ,故
,故.files/image644.gif) 在
在.files/image646.gif) 上是減函數,
上是減函數,
又當.files/image209.gif) 、
、.files/image211.gif) 、
、.files/image038.gif) 、
、.files/image283.gif) 是正實數時,
是正實數時,.files/image648.gif)
∴.files/image650.gif) .
.
由.files/image644.gif) 的單調性有:
的單調性有:.files/image652.gif) ,
,
即.files/image654.gif) .…………12′
.…………12′
20.(本小題滿分13分)
如圖,已知曲線.files/image289.gif) 與拋物線
與拋物線.files/image291.gif) 的交點分別為
的交點分別為.files/image042.gif) 、
、.files/image044.gif) ,曲線
,曲線.files/image293.gif) 和拋物線
和拋物線.files/image295.gif) 在點
在點.files/image042.gif) 處的切線分別為
處的切線分別為.files/image298.gif) 、
、.files/image300.gif) ,且
,且.files/image298.gif) 、
、.files/image300.gif) 的斜率分別為
的斜率分別為.files/image302.gif) 、
、.files/image304.gif) .
.
(Ⅰ)當.files/image306.gif) 為定值時,求證
為定值時,求證.files/image308.gif) 為定值(與
為定值(與.files/image310.gif) 無關),并求出這個定值;
無關),并求出這個定值;
(Ⅱ)若直線.files/image300.gif) 與
與.files/image177.gif) 軸的交點為
軸的交點為.files/image313.gif) ,當
,當.files/image315.gif) 取得最小值
取得最小值.files/image317.gif) 時,求曲線
時,求曲線.files/image293.gif) 和
和.files/image295.gif) 的方程。
的方程。
【解】(Ⅰ)設點.files/image042.gif) 的坐標為
的坐標為.files/image657.gif) ,
,
由.files/image659.gif) 得:
得:.files/image661.gif)
則.files/image663.gif) ,∴
,∴.files/image665.gif) …………2′
…………2′
由.files/image667.gif) 得
得.files/image669.gif) ,∴
,∴ .files/image671.gif) …………4′
…………4′
∴.files/image673.gif)
又∵.files/image675.gif) ,
,.files/image677.gif) ,∴
,∴.files/image679.gif) .
.
∴
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com