
題目列表(包括答案和解析)
| a |
| b |
| OP |
| OA |
| OB |
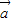 =(x-2,y),
=(x-2,y),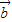 =(x+2,y),且|a|+|b|=8,
=(x+2,y),且|a|+|b|=8,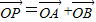 (O為坐標原點),是否存在直線l,使得四邊形OAPB為矩形,若存在,求出直線l的方程,若不存在,請說明理由.
(O為坐標原點),是否存在直線l,使得四邊形OAPB為矩形,若存在,求出直線l的方程,若不存在,請說明理由.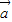 =(x-2,y),
=(x-2,y),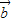 =(x+2,y),且|a|+|b|=8,
=(x+2,y),且|a|+|b|=8,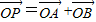 (O為坐標原點),是否存在直線l,使得四邊形OAPB為矩形,若存在,求出直線l的方程,若不存在,請說明理由.
(O為坐標原點),是否存在直線l,使得四邊形OAPB為矩形,若存在,求出直線l的方程,若不存在,請說明理由.| a |
| b |
| OP |
| OA |
| OB |
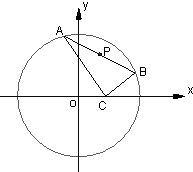 已知點C(1,0),點A、B是⊙O:x2+y2=9上任意兩個不同的點,且滿足
已知點C(1,0),點A、B是⊙O:x2+y2=9上任意兩個不同的點,且滿足| AC |
| BC |
一、選擇題
1―5 CADBA 6―10 CBABD 11―12 CC
二、填空題
13.(理)--數學(文科和理科).files/image166.gif) (文)(―1,1) 14.
(文)(―1,1) 14.--數學(文科和理科).files/image168.gif) 15.(理)18(文)(1,0)
15.(理)18(文)(1,0)
16.①③
三、解答題
17.解:(1)由題意得--數學(文科和理科).files/image170.gif) ………………2分
………………2分
--數學(文科和理科).files/image172.gif)
(2)由--數學(文科和理科).files/image174.gif) 可知A、B都是銳角,
…………7分
可知A、B都是銳角,
…………7分
--數學(文科和理科).files/image176.gif)
這時三角形為有一頂角為120°的等腰三角形 …………12分
18.(理)解:(1)ξ的所有可能的取值為0,1,2,3。 ………………2分
--數學(文科和理科).files/image178.gif)
(2)--數學(文科和理科).files/image180.gif) ………………12分
………………12分
(文)解:(1)--數學(文科和理科).files/image182.gif) ; ………………6分
; ………………6分
(2)因為--數學(文科和理科).files/image184.gif)
--數學(文科和理科).files/image186.gif) …………10分
…………10分
所以--數學(文科和理科).files/image188.gif) …………12分
…………12分
19.解:(1)--數學(文科和理科).files/image190.gif) ,
………………1分
,
………………1分
依題意知,--數學(文科和理科).files/image192.gif) ………………3分
………………3分
(2)令--數學(文科和理科).files/image194.gif) …………4分
…………4分
--數學(文科和理科).files/image196.gif) …………5分
…………5分
所以,--數學(文科和理科).files/image198.gif) …………7分
…………7分
(3)由上可知--數學(文科和理科).files/image200.gif)
①當--數學(文科和理科).files/image202.gif) 恒成立,
恒成立,
必須且只須--數學(文科和理科).files/image204.gif) , …………8分
, …………8分
--數學(文科和理科).files/image206.gif) ,
,
則--數學(文科和理科).files/image208.gif) ………………9分
………………9分
②當--數學(文科和理科).files/image210.gif) ……10分
……10分
要使當--數學(文科和理科).files/image212.gif)
綜上所述,t的取值范圍是--數學(文科和理科).files/image214.gif) ………………12分
………………12分
20.解法一:(1)取BB1的中點D,連CD、AD,則∠ACD為所求。…………1分
--數學(文科和理科).files/image216.gif)
(2)方法一 作CE⊥AB于E,C1E1⊥A1B1于E1,連EE1,
則AB⊥面CC1E1E,因此平面PAB⊥面CC1E1E。
因為A1B1//AB,所以A1B1//平面PAB。則只需求點E1到平面PAB的距離。
作E1H⊥EP于H,則E1H⊥平面PAB,則E1H即為所求距離。 …………6分
求得--數學(文科和理科).files/image218.gif) …………8分
…………8分
方法二:設B1到平面PAB的距離為h,則由--數學(文科和理科).files/image220.gif)
得--數學(文科和理科).files/image222.gif) ………………8分
………………8分
(3)設平面PAB與平面PA1B1的交線為l,由(2)知,A1B1//平面PAB,
則A1B1//l,因為AB⊥面CC1E1E,則l⊥面CC1E1E,
所以∠EPE1就是二面有AB―P―A1B的平面角。 ………………9分
要使平面PAB⊥平面PA1B1,只需∠EPE1=90°。 ………………10分
在矩形CEE--數學(文科和理科).files/image224.gif)
解得--數學(文科和理科).files/image226.gif)
|