日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

△ABC中，內角A、B、C成等差數列，其對邊a、b、c滿足，求A。

【解析】本試題主要考查了解三角形的運用，

因為

【點評】該試題從整體來看保持了往年的解題風格，依然是通過邊角的轉換，結合了三角形的內角和定理的知識，以及正弦定理和余弦定理，求解三角形中的角的問題。試題整體上比較穩定，思路也比較容易想，先將利用等差數列得到角B，然后利用余弦定理求解運算得到A。

已知是等差數列，其前n項和為S_n，是等比數列，且，.

（Ⅰ）求數列與的通項公式；

（Ⅱ）記，，證明（）.

【解析】（1）設等差數列的公差為d，等比數列的公比為q.

由，得，，.

由條件，得方程組，解得

所以，，.

（2）證明：（方法一）

由（1）得

     ①

   ②

由②-①得

而

故，

（方法二：數學歸納法）

①  當n=1時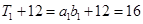，，，故等式成立.

②  假設當n=k時等式成立，即，則當n=k+1時，有：

即，因此n=k+1時等式也成立

由①和②，可知對任意，成立.

（本題16分）某國采用養老儲備金制度，公民在就業的第一年就交納養老儲備金，數目為a₁，以后每年交納的數目均比上一年增加 d（d>0）, 因此，歷年所交納的儲備金數目a₁, a₂, … 是一個公差為 d  的等差數列.  與此同時，國家給予優惠的計息政府，不僅采用固定利率，而且計算復利. 這就是說，如果固定年利率為r（r>0）,那么, 在第n年末，第一年所交納的儲備金就變為 a₁（1+r）^n－1，第二年所交納的儲備金就變成 a₂（1+r）^n－2，……. 以T_n表示到第n年末所累計的儲備金總額.（Ⅰ）寫出T_n與T_n－1（n≥2）的遞推關系式；（Ⅱ）求證T_n=A_n+ B_n，其中{A_n}是一個等比數列，{B_n}是一個等差數列.

給出下列命題：①正角的三角函數值是正的，負角的三角函數值是負的；②設P(x，y)是角a終邊上的一點，因為，所以a的正弦值與點P的縱坐標y成正比；③若sinq ×cosq>0，則q一定在第一象限；④兩個角的差是2p的整數倍，則這兩個角的同一個三角函數的值必相等；⑤若角a的終邊在y軸上，則角a的正弦線是單位長度的有向線段，其中正確命題的序號是________。（將正確的都寫出來）