日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

(II)求二面角B―PA―C的大小. 【查看更多】

 

題目列表(包括答案和解析)

（本小題滿分13分）

        已知某幾何體的三視圖如圖所示，其中分別是該幾何體的一個頂點P在三個投影面上的投影，分別是另四個頂點A，B，C，D的投影。

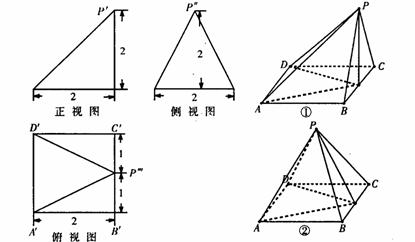
   （I）從①②兩個圖中選擇出該幾何體的直觀圖；

   （II）求直線PA與平面PBC所成角的正弦值；

   （III）設平面PAD與平面ABC的交線為，求二面角A——B的大小。

查看答案和解析>>

己知在銳角ΔABC中，角所對的邊分別為，且

(I )求角大小；

(II)當時，求的取值范圍.

20．如圖1，在平面內，是的矩形，是正三角形，將沿折起，使如圖2，為的中點，設直線過點且垂直于矩形所在平面，點是直線上的一個動點，且與點位于平面的同側。

（1）求證：平面；

（2）設二面角的平面角為，若，求線段長的取值范圍。

 


21.已知A，B是橢圓的左，右頂點，，過橢圓C的右焦點F的直線交橢圓于點M，N，交直線于點P，且直線PA，PF，PB的斜率成等差數列,R和Q是橢圓上的兩動點，R和Q的橫坐標之和為2，RQ的中垂線交X軸于T點

(1)求橢圓C的方程；

（2）求三角形MNT的面積的最大值

22. 已知函數 ，

（Ⅰ）若在上存在最大值與最小值，且其最大值與最小值的和為，試求和的值。

（Ⅱ）若為奇函數：

（1）是否存在實數，使得在為增函數，為減函數，若存在，求出的值，若不存在，請說明理由；

（2）如果當時，都有恒成立，試求的取值范圍.

查看答案和解析>>

 

一、選擇題：

       DDABD  ACCBB  CD

二、填空題：

13．高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。   14．高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。   15．32    16． 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

三、解答題：

17．解：（I）高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。服從超幾何分布

       高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

       高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。       3分

   （II）高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。    5分

       高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。    7分

       高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。       9分

Y

5

6

7

P

高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

    …………10分

          
   
          
    
    
          
    
          高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
          18．解：（Ｉ）取ＣＤ中點Ｆ，連接ＥＦ，
                 則高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。  高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。         4分
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。平面PAC       6分
             （II）以點C為坐標原點，分別以CD，CB，CP為x軸，y軸，z軸建立空間直角坐標系高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，
                 則高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。平面PAC
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。    
8分
                 設平面PAB的一個法向量為高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，
                 由高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，
                 得高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 不妨令高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，
                 即高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。       10分
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。    
12分
          19．解：（I）高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。是等差數列
                 又高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。    2分
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。    
5分
                 又高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。為首項，以高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。為公比的等比數列     
6分
             （II）高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 當高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 又高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。                高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。是單調遞增數列     
9分
             （III）高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。時,高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 即高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。       12分
          20．解：（I）高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
          高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
          0
          （0，1）
          1
          （1，3）
          3
          高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
           
          +
          0
          -
           
          高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
          0
          高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
          1
          高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
          高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。    3分
             （II）設高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。時，函數高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。的值域為A，
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，
                 總存在高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
             （1）當高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。時，
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。上單調遞減，
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。    6分
             （2）當高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。時，
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 令高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。（舍去）
                 ①當高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。時，列表如下：
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
          0
          高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
          高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
          高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
          3
          高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
           
          -
          0
          +
           
          高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
          0
          高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
          高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
          高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
          高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。若高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，
                 則高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。    
9分
                 ②當高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。時，高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。時，
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。函數高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。上單調遞減
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。       11分
                 綜上，實數高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。的取值范圍是高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。     
12分
          21．解：（I）高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。    2分
             （II）設點高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 直線高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。的方程為高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 代入高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 整理，得高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。是方程的兩個相等實根
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 解，得高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。       6分
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 令高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，得點A的坐標為高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 又高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。   高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 又直線高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 令高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，得點B的坐標為高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。     
8分
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 整理，得高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。     
10分
                 令高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。以AB為直徑的圓恒過定點（1，0）和（-1，0）。      12分
          22．A．解：（I）高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，
                 又高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。     
3分
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。       7分
             （II）高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。        10分
          B．解：（I）高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。       2分
                 即高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
              高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。     
4分
             （II）高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。       6分
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 即高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。       8分
                 兩邊平方，得高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 解，得高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。     
10分
          C．解：（I）原不等式等價于
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 或高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。       3分
                 解，得高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。
                 即不等式的解集為高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。   6分
             （II）高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。    8分
                 高考資源網( www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。     
10分
          		
          
	
	

          
	




主站蜘蛛池模板：
91麻豆精品国产91久久久资源速度
|
五月婷婷中文
|
狠狠视频
|
国产欧美一区二区
|
国产不卡一二三区
|
国产精品久久久久久久久久妞妞
|
久久久久久亚洲
|
欧美激情视频久久
|
国产精品亚洲第一区在线暖暖韩国
|
亚洲天堂久久
|
羞羞视频在线观看免费
|
欧美久久久久久久久中文字幕
|
天堂亚洲
|
欧美国产精品一区
|
黑人精品视频
|
日本中文在线
|
久久久精品国产
|
欧美成人a
|
久久久久久久久免费视频
|
午夜影视在线观看
|
亚洲精品在线看
|
亚洲精品乱码久久久久久9色
|
成人看的羞羞视频免费观看
|
风间由美一区二区三区在线观看
|
日韩在线视频精品
|
成人精品一区二区
|
中文在线播放
|
久久水蜜桃
|
色精品|
国产精品日产欧美久久久久
|
国产日韩欧美一区
|
国产黄色大片
|
国产精品久久久久久久久
|
欧美3区|
欧美精品在线观看免费
|
色噜噜色偷偷
|
精品在线看
|
一区二区免费在线观看
|
久久久久久久成人
|
久久伊人一区
|
久久伊人成人
|