
題目列表(包括答案和解析)
如圖,在正方體 中,
中,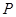 是棱
是棱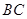 的中點,
的中點,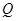 在棱
在棱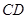 上.
上.
且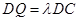 ,若二面角
,若二面角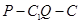 的余弦值為
的余弦值為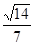 ,求實數
,求實數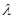 的值.
的值.
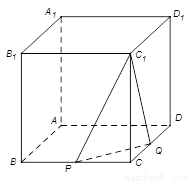
【解析】以A點為坐標原點,AB為x軸,AD為y軸,AA1為z軸,建立空間直角坐標系,設正方體的棱長為4,分別求出平面C1PQ法向量和面C1PQ的一個法向量,然后求出兩法向量的夾角,建立等量關系,即可求出參數λ的值.
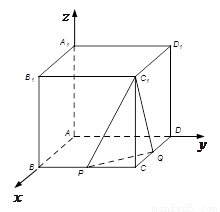
| PQ |
| PC |
| PQ |
| PC |
| AB |
| DA |
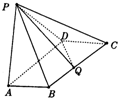 如圖,四棱錐P-ABCD中,底面ABCD是矩形,AB=
如圖,四棱錐P-ABCD中,底面ABCD是矩形,AB=| 3 |
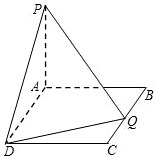
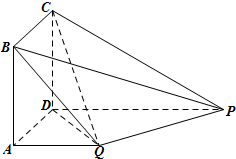 如圖,四邊形ABCD為正方形,在四邊形ADPQ中,PD∥QA.又QA⊥平面ABCD,QA=AB=
如圖,四邊形ABCD為正方形,在四邊形ADPQ中,PD∥QA.又QA⊥平面ABCD,QA=AB=| 1 | 2 |
 如圖,在矩形ABCD中,AB=2,BC=a,又PA⊥平面ABCD,PA=4.
如圖,在矩形ABCD中,AB=2,BC=a,又PA⊥平面ABCD,PA=4.湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com