
題目列表(包括答案和解析)
D
解析:當x>0時,![]() ,即
,即![]() 令
令![]() ,
,
則函數![]() 在區間(0,+∞)上為減函數,又
在區間(0,+∞)上為減函數,又![]() 在定義域上是奇函數,
在定義域上是奇函數,
∴函數![]() 在定義域上是偶函數,且
在定義域上是偶函數,且![]() ,則
,則![]() >0在(0,+∞)上的解集是(0,2);
>0在(0,+∞)上的解集是(0,2);
函數![]() 是定義域上的奇函數,則
是定義域上的奇函數,則![]() >0的解集是(-∞,-2)∪(0,2).
>0的解集是(-∞,-2)∪(0,2).
D
解析:當x>0時,![]() ,即
,即![]() 令
令![]() ,
,
則函數![]() 在區間(0,+∞)上為減函數,又
在區間(0,+∞)上為減函數,又![]() 在定義域上是奇函數,
在定義域上是奇函數,
∴函數![]() 在定義域上是偶函數,且
在定義域上是偶函數,且![]() ,則
,則![]() >0在(0,+∞)上的解集是(0,2);
>0在(0,+∞)上的解集是(0,2);
函數![]() 是定義域上的奇函數,則
是定義域上的奇函數,則![]() >0的解集是(-∞,-2)∪(0,2).
>0的解集是(-∞,-2)∪(0,2).
D
解析:當x>0時,![]() ,即
,即![]() 令
令![]() ,
,
則函數![]() 在區間(0,+∞)上為減函數,又
在區間(0,+∞)上為減函數,又![]() 在定義域上是奇函數,
在定義域上是奇函數,
∴函數![]() 在定義域上是偶函數,且
在定義域上是偶函數,且![]() ,則
,則![]() >0在(0,+∞)上的解集是(0,2);
>0在(0,+∞)上的解集是(0,2);
函數![]() 是定義域上的奇函數,則
是定義域上的奇函數,則![]() >0的解集是(-∞,-2)∪(0,2).
>0的解集是(-∞,-2)∪(0,2).
已知函數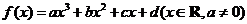 ,
,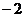 是
是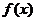 的一個零點,又
的一個零點,又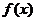 在
在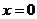 處有極值,在區間
處有極值,在區間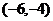 和
和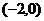 上是單調的,且在這兩個區間上的單調性相反.(1)求
上是單調的,且在這兩個區間上的單調性相反.(1)求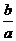 的取值范圍;(2)當
的取值范圍;(2)當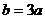 時,求使
時,求使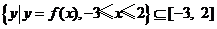 成立的實數
成立的實數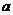 的取值范圍.
的取值范圍.
從而 或
或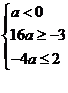 即
即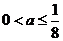 或
或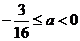
所以存在實數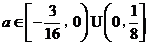 ,滿足題目要求.……………………12分
,滿足題目要求.……………………12分
設橢圓  :
: (
( )的一個頂點為
)的一個頂點為 ,
, ,
, 分別是橢圓的左、右焦點,離心率
分別是橢圓的左、右焦點,離心率
 ,過橢圓右焦點
,過橢圓右焦點
 的直線
的直線  與橢圓
與橢圓  交于
交于 ,
, 兩點.
兩點.
(1)求橢圓 的方程;
的方程;
(2)是否存在直線  ,使得
,使得
 ,若存在,求出直線
,若存在,求出直線
 的方程;若不存在,說明理由;
的方程;若不存在,說明理由;
【解析】本試題主要考查了橢圓的方程的求解,以及直線與橢圓的位置關系的運用。(1)中橢圓的頂點為 ,即
,即 又因為
又因為 ,得到
,得到 ,然后求解得到橢圓方程(2)中,對直線分為兩種情況討論,當直線斜率存在時,當直線斜率不存在時,聯立方程組,結合
,然后求解得到橢圓方程(2)中,對直線分為兩種情況討論,當直線斜率存在時,當直線斜率不存在時,聯立方程組,結合 得到結論。
得到結論。
解:(1)橢圓的頂點為 ,即
,即
 ,解得
,解得 ,
,
 橢圓的標準方程為
橢圓的標準方程為 --------4分
--------4分
(2)由題可知,直線 與橢圓必相交.
與橢圓必相交.
①當直線斜率不存在時,經檢驗不合題意. --------5分
②當直線斜率存在時,設存在直線 為
為 ,且
,且 ,
, .
.
由 得
得 , ----------7分
, ----------7分
 ,
, ,
,

=
所以 ,
----------10分
,
----------10分
故直線 的方程為
的方程為 或
或
即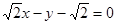 或
或
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com