題目列表(包括答案和解析)
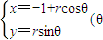為參數r＞0），以O為極點，x軸正半軸為極軸建立極坐標系，直線l的極坐標方程為
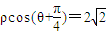．若直線l與圓C相切，求r的值．
．
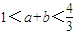（2012•徐州模擬）本題包括A、B、C、D四小題，請選定其中兩題，并在答題卡指定區域內作答，
|
|
| π |
| 4 |
| 2 |
| 4 |
| 3 |
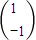在矩陣M=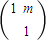
變換下得到的向量是
．
，
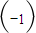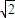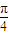），曲線C的參數方程為
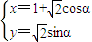（α為參數）．
|
|
|
| 2 |
| π |
| 4 |
|
平移可得曲線（x+1）2-（y-3）2=1；
，則動點P的軌跡為雙曲線；
與
夾角為銳角θ，且滿足 
，則點P的軌跡是圓（除去與直線AB的交點）；說明：
一、本解答給出了每題要考查的主要知識和能力，并給出了一種或幾種解法供參考，如果考生的解法與本解答不同，可根據試題的主要考查內容比照評分標準制定相應的評分細則。
二、對計算題，當考生的解答在某一步出現錯誤時，如果后續部分的解答未改變該題的內容和難度，可視影響的程度決定后續部分的給分，但不得超過該部分正確解答所給分數的一半；如果后續部分的解答存在較嚴重的錯誤，則不再給分。
三、解答右端所注分數，表示考生正確做到這一步應得的累加分數。
四、每題只給整數分數，選擇題和填空題不給中間分。
一、選擇題：
題號
1
2
3
4
5
6
7
8
9
10
答案
B
C
C
D
A
A
B
C
B
D
二、填空題：
11．40.6,1.1 12．
13．
14．30 15． 
16．（1，1），（2，2），（3，4），（4，8）
三、解答題：
17．（Ⅰ）
， ①
…………………2分
又
， ∴
②
……………… 4分
由①、②得
…………………………………………………………… 6分
（Ⅱ）
……………………………………… 8分
…………………………………………………………………… 10分
…………………………………………………………………………12分
18．（Ⅰ）設點
，則
，
，
，又
，
，∴橢圓的方程為：
…………………………………………7分
（Ⅱ）當過
直線
的斜率不存在時，點
，則
；
當過直線的斜率存在時，設斜率為
，則直線的方程為
，
設
，由
得：
…………………………………………10分
……13分
綜合以上情形，得：
……………………………………………………14分
|
面EFG，PB
平面EFG，
，
，又GM=
，………………7分
………………8分
，
………………………………9分
，則
，
…………………………13分
故存在點Q，當CQ=
時，點A到平面EFQ的距離為0.8. ……………………… 14分
…………1分
， 即
，
……………3分
，∴PB∥平面EFG. ………………………………………………………… 4分
,
…………………………………………5分
，
……………………… 8分
……………………………………10分
， 設平面EFQ的法向量為
，則
， ……………………………………………………12分
， ∴點A到平面EFQ的距離
，……13分
，
不合題意，舍去.
，
………………2分
時，
， …………4分
是單調增函數； ………………6分
是單調減函數； ………………8分
是偶函數，對任意
都有
成立
對任意
或
時，
是定義域上的單調函數，
時，對任意
時，
，由
上是單調增函數
在上是單調減函數，∴對任意
時，對任意
時，對任意
}的公差是
，則
，解得
……………………………………2分
=－1＜0
適合條件①；又
，所以當
=4或5時，
取得最大值20，即
…………………………………………4分
，所以當n≥3時，
，此時數列
單調遞減；當
，即
，所以
≥7………………………………………………………8分
成立，
的各項均為正整數，可得
……………10分
……11分
…13分
……………………………………………15分
，總有
，故有
，這與數列（
）的各項均為正整數矛盾！
,都有
成立. ………………………16分