
題目列表(包括答案和解析)
定義在 上的函數
上的函數 對任意
對任意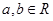 都有
都有 (
(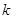 為常數).
為常數).
(1)判斷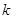 為何值時
為何值時 為奇函數,并證明;
為奇函數,并證明;
(2)設 ,
, 是
是 上的增函數,且
上的增函數,且 ,若不等式
,若不等式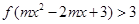 對任意
對任意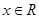 恒成立,求實數
恒成立,求實數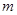 的取值范圍.
的取值范圍.
定義在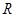 上的函數
上的函數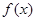 對任意
對任意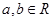 都有
都有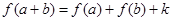 (
(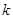 為常數).
為常數).
(1)判斷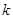 為何值時
為何值時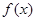 為奇函數,并證明;
為奇函數,并證明;
(2)設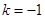 ,
,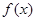 是
是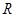 上的增函數,且
上的增函數,且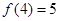 ,若不等式
,若不等式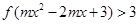 對任意
對任意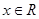 恒成立,求實數
恒成立,求實數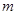 的取值范圍.
的取值范圍.
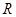 上的函數
上的函數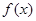 對任意
對任意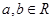 都有
都有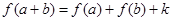 (
(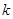 為常數).
為常數).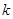 為何值時
為何值時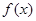 為奇函數,并證明;
為奇函數,并證明;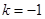 ,
,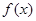 是
是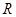 上的增函數,且
上的增函數,且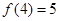 ,若不等式
,若不等式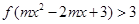 對任意
對任意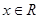 恒成立,求實數
恒成立,求實數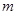 的取值范圍.
的取值范圍.已知方程tan2x一 tan
x+1=0在x
tan
x+1=0在x [0,n
[0,n )( n
)( n N*)內所有根的和記為an
N*)內所有根的和記為an
(1)寫出an的表達式;(不要求嚴格的證明)
(2)記Sn = a1 + a2 +…+ an求Sn;
(3)設bn =(kn一5)  ,若對任何n
,若對任何n N* 都有an
N* 都有an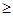 bn,求實數k的取值范圍.
bn,求實數k的取值范圍.
已知方程tan2x一 tan x+1=0在x
tan x+1=0在x [0,n
[0,n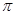 )( n
)( n N*)內所有根的和記為an
N*)內所有根的和記為an
(1)寫出an的表達式;(不要求嚴格的證明)
(2)記Sn = a1 + a2 +…+ an求Sn;
(3)設bn =(kn一5) 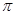 ,若對任何n
,若對任何n N* 都有an
N* 都有an bn,求實數k的取值范圍.
bn,求實數k的取值范圍.
1.A2.C3.B4.D 5.C 6.B 7.D8.B9.B10.D11.A12.D13.C
13. 14.
14. 15.
15. 16.
16. 
17.(1) ――2分
――2分
 ――2分
――2分
 ;
――2分
;
――2分
(II) ――2分
――2分

18.(Ⅰ)證明:  平面
平面 平面
平面 ,
, ,
,
平面 平面
平面 =
= ,
,
 平面
平面 ,
,
 平面
平面 ,
, ,……… 2分
,……… 2分
又 為圓
為圓 的直徑,
的直徑, ,
…………………… 4分
,
…………………… 4分
 平面
平面 。
…………………… 5分
。
…………………… 5分
(Ⅱ)設 的中點為
的中點為 ,則
,則

 ,又
,又

 ,
,
則

 ,
, 為平行四邊形,
…………………… 6分
為平行四邊形,
…………………… 6分

 ,又
,又 平面
平面 ,
, 平面
平面 ,
,
 平面
平面 。
……………………8分
。
……………………8分
(Ⅲ)過點 作
作 于
于 ,
, 平面
平面 平面
平面 ,
,
 平面
平面 ,
, , …………………… 9分
, …………………… 9分
 平面
平面 ,
,

 ,………………… 11分
,………………… 11分

 .
…………………… 12分
.
…………………… 12分
19.解:(1)解方程得 或
或 1分
1分
 當
當 時,
時, 或
或 ,此時
,此時 2分
2分
當 時,
時, 3分
3分
依次類推:
 5分
5分
(2)

 9分
9分
(3)由 得
得


 11分
11分
設
易證 在
在 上單調遞減,在(
上單調遞減,在( )上單調遞增。 13分
)上單調遞增。 13分



 15分
15分
20.解:(Ⅰ)設第二關不過關事件為 ,則事件
,則事件 是指第二關出現點數之和沒有大于
是指第二關出現點數之和沒有大于 ,由第二關出現點數之和為2,3的次數分別為1,2知:
,由第二關出現點數之和為2,3的次數分別為1,2知: …4分
…4分
答: 第二關未過關的概率為 。………………5分
。………………5分
(Ⅱ)設第三關不過關事件為 ,則第三關過關事件為
,則第三關過關事件為
由題設知:事件 是指第三關出現點數之和沒有大于
是指第三關出現點數之和沒有大于 ,………7分
,………7分
由第三關出現點數之和為3,4,5的次數分別為1,3,6知: ……9分
……9分
∴ ………………11分
………………11分
答: 第三關過關的概率為 .………………12分
.………………12分
21.解:(Ⅰ)函數 的導數為
的導數為 ,
,
由題意可知 對于
對于 恒成立, 即
恒成立, 即 對于
對于 恒成立,
恒成立,
可得 。
。
另解:函數 的導數為
的導數為 ,當
,當 時
時 恒成立;當
恒成立;當 時,
時,
由 得
得 ,則函數的單調增區間為
,則函數的單調增區間為 與
與 ,
,
則當 ,即
,即 時滿足條件。
時滿足條件。
(Ⅱ)由(Ⅰ)知 ,
,
過點A(1,0)作曲線C的切線,設切點 ,則切線方程為:
,則切線方程為:
將 代入得:
代入得:
即 (*)
(*)
則 或
或 故滿足條件的切線只有兩條,且它們的斜率分別為
故滿足條件的切線只有兩條,且它們的斜率分別為 與
與 ,則由
,則由
 得
得 
22.解:(Ⅰ)設橢圓方程為 ,則
,則
 ,得
,得 ………2分
………2分
所以橢圓方程為 ,拋物線方程為
,拋物線方程為 。
。
另解:過 作垂直于
作垂直于 軸的直線
軸的直線 ,即拋物線的準線,作
,即拋物線的準線,作 垂直于該準線,
垂直于該準線,
作 軸于
軸于 ,則由拋物線的定義得
,則由拋物線的定義得 ,
,
所以

 ,
,
得 ,所以c=1,
,所以c=1,
所以橢圓方程為 ,
,
拋物線方程為 。
。
(Ⅱ)設 ,直線
,直線 ,代入
,代入 得:
得: ,即
,即 ,
,
則 …………………………………………9分
…………………………………………9分
同理,將 代入
代入 得:
得: ,
,
則 , ……………………………………………………11分
, ……………………………………………………11分
所以 =
=
 為定值。
…………………………………………………………………15分
為定值。
…………………………………………………………………15分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com