日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

7、9、10班同學做乙題，其他班同學任選一題，若兩題都做，則以較少得分計入總分．

（甲）已知f(x)=ax－ln(－x)，x∈[－e，0），，其中e=2.718 28…是自然對數的底數，a∈R.

（1）若a=－1，求f(x)的極值；

（2）求證：在（1）的條件下，；

（3）是否存在實數a，使f(x)的最小值是3，如果存在，求出a的值；如果不存在，說明理由.

（乙）定義在（0，＋∞）上的函數，其中e=2.718 28…是自然對數的底數，a∈R.

   （1）若函數f(x)在點x=1處連續，求a的值；

（2）若函數f(x)為（0，1）上的單調函數，求實數a的取值范圍；并判斷此時函數f(x)在（0，＋∞）上是否為單調函數；

（3）當x∈（0，1）時，記g(x)=lnf(x)＋x²－ax. 試證明：對，當n≥2時，有

解：：因為，所以f(1)f(2)<0，因此f(x)在區間（1，2）上存在零點，又因為y=與y=-在（0，+）上都是增函數，因此在（0，+）上是增函數，所以零點個數只有一個方法2：把函數的零點個數個數問題轉化為判斷方程解的個數問題，近而轉化成判斷與交點個數問題，在坐標系中畫出圖形

由圖看出顯然一個交點，因此函數的零點個數只有一個

袋中有50個大小相同的號牌，其中標著0號的有5個，標著n號的有n個（n=1,2,…9）,現從袋中任取一球，求所取號碼的分布列，以及取得號碼為偶數的概率.

某市為了了解今年高中畢業生的體能狀況，從本市某校高中畢業班中抽取一個班進行鉛球測試，成績在8.0米（精確到0.1米）以上的為合格．把所得數據進行整理后，分成6組畫出頻率分布直方圖的一部分（如圖），已知從左到右前5個小組的頻率分別為0.04，0.10，0.14，0.28，0.30．第6小組的頻數是7．
（1）求這次鉛球測試成績合格的人數；
（2）若由直方圖來估計這組數據的中位數，指出它在第幾組內，并說明理由；
（3）若參加此次測試的學生中，有9人的成績為優秀，現在要從成績優秀的學生中，隨機選出2人參加“畢業運動會”，已知a、b的成績均為優秀，求兩人至少有1人入選的概率．

某市為了了解今年高中畢業生的體能狀況，從本市某校高中畢業班中抽取一個班進行鉛球測試，成績在8.0米(精確到0.1米)以上的為合格.把所得數據進行整理后，分成6組畫出頻率分布直方圖的一部分(如圖)，已知從左到右前5個小組的頻率分別為0.04，0.10，0.14，0.28，0.30.第6小組的頻數是7.

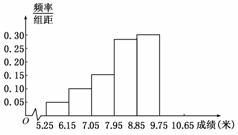
(1) 求這次鉛球測試成績合格的人數；

(2) 若由直方圖來估計這組數據的中位數，指出它在第幾組內，并說明理由；

(3) 若參加此次測試的學生中，有9人的成績為優秀，現在要從成績優秀的學生中，隨機選出2人參加“畢業運動會”，已知、的成績均為優秀，求兩人至少有1人入選的概率.