
題目列表(包括答案和解析)
直線![]() 與圓
與圓![]() 相交于兩點M、N, 若滿足
相交于兩點M、N, 若滿足![]() , 則
, 則![]() ·
·![]() (O為坐標原點)等于 ( )
(O為坐標原點)等于 ( )
A. -2 B. -1 C. 0 D. 1
直線![]() 與圓
與圓![]() 相交于兩點M、N, 若滿足
相交于兩點M、N, 若滿足![]() , 則
, 則![]() ·
·![]() (O為坐標原點)等于 ( )
(O為坐標原點)等于 ( )
A. -2 B. -1 C. 0 D. 1
直線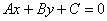 與圓
與圓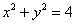 相交于兩點M、N,若滿足
相交于兩點M、N,若滿足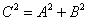 , 則
, 則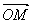 ·
·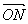 (O為坐標原點)等于 ( )
(O為坐標原點)等于 ( )
A.-2 B.-1 C.0 D.1
若圓C過點M(0,1)且與直線l:y=-1相切,設圓心C的軌跡為曲線E,A、B(A在y軸的右側)為曲線E上的兩點,點P(0,t)(t>0),且滿足![]() =λ
=λ![]() (λ>1).
(λ>1).
(Ⅰ)求曲線E的方程;
(Ⅱ)若t=6,直線AB的斜率為![]() ,過A、B兩點的圓N與拋物線在點A處共同的切線,求圓N的方程;
,過A、B兩點的圓N與拋物線在點A處共同的切線,求圓N的方程;
(Ⅲ)分別過A、B作曲線E的切線,兩條切線交于點Q,若點Q恰好在直線l上,求證:t與![]() ·
·![]() 均為定值.
均為定值.
| AP |
| PB |
| 1 |
| 2 |
| QA |
| QB |
一、選擇題:
1.解析:B.由 且
且 能夠推出
能夠推出 ;反之,由
;反之,由 只能推出
只能推出 或
或 ,而不能推出
,而不能推出 且
且 .故“
.故“ ”是“
”是“ 且
且 ”的必要不充分條件,故選B.
”的必要不充分條件,故選B.
評析:有關充要條件的判定問題,概念性較強,進行判斷時,必須緊扣概念.一方面,要正確理解充要條件本身的概念,進行雙向推理,準確判斷;另一方面,還要注意根據具體問題所涉及到的數學概念來思考.本題中,弄清并集和交集概念中“或”與“且”的關系顯得很重要.
|