
題目列表(包括答案和解析)
解:(1)由拋物線C1:![]() 得頂點P的坐標為(2,5)………….1分
得頂點P的坐標為(2,5)………….1分
 ∵點A(-1,0)在拋物線C1上∴
∵點A(-1,0)在拋物線C1上∴![]() .………………2分
.………………2分
(2)連接PM,作PH⊥x軸于H,作MG⊥x軸于G..
∵點P、M關于點A成中心對稱,
∴PM過點A,且PA=MA..
∴△PAH≌△MAG..
∴MG=PH=5,AG=AH=3.
∴頂點M的坐標為(![]() ,5).………………………3分
,5).………………………3分
∵拋物線C2與C1關于x軸對稱,拋物線C3由C2平移得到
∴拋物線C3的表達式![]() . …………4分
. …………4分
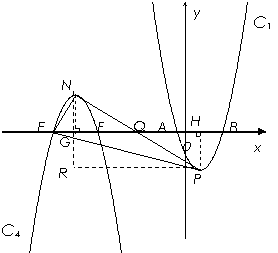
(3)∵拋物線C4由C1繞x軸上的點Q旋轉180°得到
∴頂點N、P關于點Q成中心對稱.
由(2)得點N的縱坐標為5.
設點N坐標為(m,5),作PH⊥x軸于H,作NG⊥x軸于G,作PR⊥NG于R.
∵旋轉中心Q在x軸上,
∴EF=AB=2AH=6.
∴EG=3,點E坐標為(![]() ,0),H坐標為(2,0),R坐標為(m,-5).
,0),H坐標為(2,0),R坐標為(m,-5).
 根據勾股定理,得
根據勾股定理,得
![]()
![]()
![]()
①當∠PNE=90º時,PN2+ NE2=PE2,
解得m=![]() ,∴N點坐標為(
,∴N點坐標為(![]() ,5)
,5)
②當∠PEN=90º時,PE2+ NE2=PN2,
解得m=![]() ,∴N點坐標為(
,∴N點坐標為(![]() ,5).
,5).
③∵PN>NR=10>NE,∴∠NPE≠90º ………7分
綜上所得,當N點坐標為(![]() ,5)或(
,5)或(![]() ,5)時,以點P、N、E為頂點的三角形是直角三角形.…………………………………………………………………………………8分
,5)時,以點P、N、E為頂點的三角形是直角三角形.…………………………………………………………………………………8分
解不等式組或方程:
(1)求不等式組![]() 的整數解;
的整數解;
(2)解一元二次方程:x2-4x+1=0(配方法)
解方程x(x-1)=2.
有學生給出如下解法:
∵x(x-1)=2=1×2=(-1)×(-2),
∴![]() 或
或![]() 或
或![]() 或
或![]()
解上面第一、四方程組,無解;解第二、三方程組,得x=2或x=-1.
∴x=2或x=-1.
請問:這個解法對嗎?試說明你的理由.如果你覺得這個解法不對,請你求出方程的解.
解方程x(x-1)=2
有學生給出如下解法:
∵x(x-1)=2=1×2=(-1)×(-2),
![]()
解上面第一、四方程組,無解;解第二、三方程組,得x=2或x=-1
∴x=2或x=-1
請問:這個解法對嗎?試說明你的理由
閱讀材料:把形如ax2+bx+c的二次三項式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆寫,即a2±2ab+b2=(a±b)2.
例如:![]() 是x2-2x+4的三種不同形式的配方(即“余項”分別是常數項、一次項、二次項——見橫線上的部分).
是x2-2x+4的三種不同形式的配方(即“余項”分別是常數項、一次項、二次項——見橫線上的部分).
請根據閱讀材料解決下列問題:
(1)比照上面的例子,寫出x2-4x+2三種不同形式的配方;
(2)將a2+ab+b2配方(至少兩種形式);
(3)已知a2+b2+c2-ab-3b-2c+4=0,求a+b+c的值.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com