
題目列表(包括答案和解析)
已知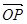 =
=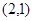 ,
,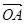 =
=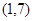 ,
, =
=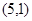 ,設
,設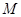 是直線
是直線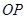 上一點,
上一點,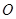 是坐標原點.
是坐標原點.
⑴求使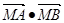 取最小值時的
取最小值時的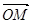 ;
⑵對(1)中的點
;
⑵對(1)中的點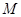 ,求
,求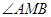 的余弦值.
的余弦值.
【解析】第一問中利用設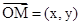 ,則根據已知條件,O,M,P三點共線,則可以得到x=2y,然后利用
,則根據已知條件,O,M,P三點共線,則可以得到x=2y,然后利用
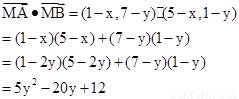
可知當x=4,y=2時取得最小值。
第二問中利用數量積的性質可以表示夾角的余弦值,進而得到結論。
(1)、因為設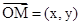 則
則
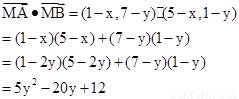
可知當x=4,y=2時取得最小值。此時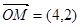 。
。
(2)
設函數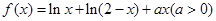 .
.
(Ⅰ) 當 時,求
時,求 的單調區間;
的單調區間;
(Ⅱ) 若 在
在 上的最大值為
上的最大值為 ,求
,求 的值.
的值.
【解析】第一問中利用函數 的定義域為(0,2),
的定義域為(0,2), .
.
當a=1時, 所以
所以 的單調遞增區間為(0,
的單調遞增區間為(0, ),單調遞減區間為(
),單調遞減區間為( ,2);
,2);
第二問中,利用當 時,
時, >0, 即
>0, 即 在
在 上單調遞增,故
上單調遞增,故 在
在 上的最大值為f(1)=a 因此a=1/2.
上的最大值為f(1)=a 因此a=1/2.
解:函數 的定義域為(0,2),
的定義域為(0,2), .
.
(1)當 時,
時, 所以
所以 的單調遞增區間為(0,
的單調遞增區間為(0, ),單調遞減區間為(
),單調遞減區間為( ,2);
,2);
(2)當 時,
時, >0, 即
>0, 即 在
在 上單調遞增,故
上單調遞增,故 在
在 上的最大值為f(1)=a 因此a=1/2.
上的最大值為f(1)=a 因此a=1/2.
若 ,計算得當
,計算得當 時
時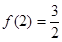 ,當
,當 時有
時有 ,
, ,
, ,
, ,因此猜測當
,因此猜測當 時,一般有不等式________________
時,一般有不等式________________
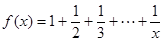 ,計算得當
,計算得當 時
時 ,當
,當 時有
時有 ,
, ,
, ,
, ,因此猜測當
,因此猜測當 時,一般有不等式________________
時,一般有不等式________________湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com