
題目列表(包括答案和解析)
參考答案:
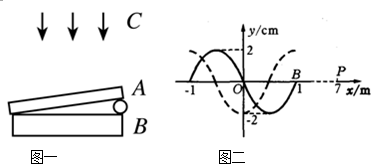
(1)甲
(2)直到P3及P1、P2的像被P4擋住,定下P4的位置
(3)1.2
評分標準:共8分,其中(1)2分,(2)(3)各3分;
| 1 |
| λ |
| 1 |
| 22 |
| 1 |
| n2 |
| 1 |
| λ |
| 1 |
| 12 |
| 1 |
| n2 |
| r2 |
| k |
| (10×10-2)2 |
| 9×109 |
| 1 |
| 2 |
| a2-4b |
| 1 |
| 2 |
| 9×10-16-4×10-15 |
(14分)
(1)開普勒行星運動第三定律指出:行星繞太陽運動的橢圓軌道的半長軸a的三次方與它的公轉周期T的二次方成正比,即![]() ,k是一個對所有行星都相同的常量。將行星繞太陽的運動按圓周運動處理,請你推導出太陽系中該常量k的表達式。已知引力常量為G,太陽的質量為M太。
,k是一個對所有行星都相同的常量。將行星繞太陽的運動按圓周運動處理,請你推導出太陽系中該常量k的表達式。已知引力常量為G,太陽的質量為M太。
(2)開普勒定律不僅適用于太陽系,它對一切具有中心天體的引力系統(如地月系統)都成立。經測定月地距離為3.84×108m,月球繞地球運動的周期為2.36×106S,試計算地球的質M地。(G=6.67×10-11Nm2/kg2,結果保留一位有效數字)
【解析】:(1)因行星繞太陽作勻速圓周運動,于是軌道的半長軸a即為軌道半徑r。根據萬有引力定律和牛頓第二定律有
![]() ①
①
于是有 ![]() ②
②
即 ![]() ③
③
(2)在月地系統中,設月球繞地球運動的軌道半徑為R,周期為T,由②式可得
![]() ④
④
解得 M地=6×1024kg ⑤
(M地=5×1024kg也算對)
23.【題文】(16分)
 如圖所示,在以坐標原點O為圓心、半徑為R的半圓形區域內,有相互垂直的勻強電場和勻強磁場,磁感應強度為B,磁場方向垂直于xOy平面向里。一帶正電的粒子(不計重力)從O點沿y軸正方向以某一速度射入,帶電粒子恰好做勻速直線運動,經t0時間從P點射出。
如圖所示,在以坐標原點O為圓心、半徑為R的半圓形區域內,有相互垂直的勻強電場和勻強磁場,磁感應強度為B,磁場方向垂直于xOy平面向里。一帶正電的粒子(不計重力)從O點沿y軸正方向以某一速度射入,帶電粒子恰好做勻速直線運動,經t0時間從P點射出。
(1)求電場強度的大小和方向。
(2)若僅撤去磁場,帶電粒子仍從O點以相同的速度射入,經![]() 時間恰從半圓形區域的邊界射出。求粒子運動加速度的大小。
時間恰從半圓形區域的邊界射出。求粒子運動加速度的大小。
(3)若僅撤去電場,帶電粒子仍從O點射入,且速度為原來的4倍,求粒子在磁場中運動的時間。
“真空中兩個靜止點電荷相距10cm,它們之間相互作用力大小為9×10-4N,當它們合在一起時,成為一個帶電量為3×10-8C的點電荷,問原來兩電荷的帶電量各為多少?”某同學求解如下:
根據電荷守恒定律:q1+q2=3×10—8C=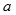 ①
①
根據庫侖定律:q1
q2=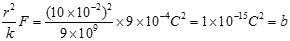
以q2=b/q1代人①式得: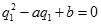
解得: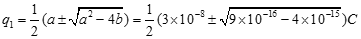
根號中的數值小于0,經檢查,運算無誤,試指出求解過程中的問題并給出正確的解答。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com