
題目列表(包括答案和解析)
(本小題滿(mǎn)分12分)如圖,已知正方體ABCD—A1B1C1D1的棱長(zhǎng)為2,E、F分別是A1B1、CC1的中點(diǎn),過(guò)D1、E、F作平面D1EGF交BB1于G。 (1)求證:EG//D1F; (2)求銳二面角C1—D1E—F的余弦值。
(本小題滿(mǎn)分12分)如圖,已知正方形ABCD和矩形ACEF所在平面互相垂直,
AB=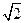 ,AF=1,M是線(xiàn)段EF的中點(diǎn)。
,AF=1,M是線(xiàn)段EF的中點(diǎn)。
(Ⅰ)求證:AM∥平面BDE;
(Ⅱ) 求二面角A-DF-B的大小.
(Ⅲ)試問(wèn):在線(xiàn)段AC上是否存在一點(diǎn)P,使得直線(xiàn)PF與AD所成角為60°?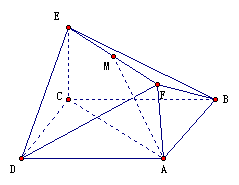
(本小題滿(mǎn)分12分)如圖,已知正方形ABCD和矩形ACEF所在平面互相垂直,
AB=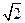 ,AF=1,M是線(xiàn)段EF的中點(diǎn)。
,AF=1,M是線(xiàn)段EF的中點(diǎn)。
(Ⅰ)求證:AM∥平面BDE;
(Ⅱ) 求二面角A-DF-B的大小.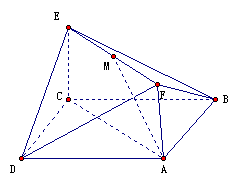
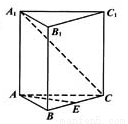
(本小題滿(mǎn)分12分)如圖,已知正三棱柱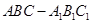 的各棱長(zhǎng)都是4,
的各棱長(zhǎng)都是4, 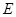 是
是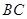 的中點(diǎn),動(dòng)點(diǎn)
的中點(diǎn),動(dòng)點(diǎn)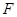 在側(cè)棱
在側(cè)棱 上,且不與點(diǎn)
上,且不與點(diǎn)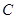 重合.
重合.
(I)當(dāng)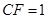 時(shí),求證:
時(shí),求證: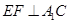 ;
;
(II)設(shè)二面角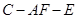 的大小為
的大小為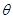 ,求
,求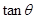 的最小值.
的最小值.
(本小題滿(mǎn)分12分)
如圖,已知正三棱柱ABC—A1B1C1的底面邊長(zhǎng)是2,D是CC1的中點(diǎn),直線(xiàn)AD與側(cè)面BB1C1C所成的角是45°.
(I)求二面角A—BD—C的大小;
(II)求點(diǎn)C到平面ABD的距離.

一、選擇題
A卷:BACDB DCABD BA
B卷:BDACD BDCAB BA
二、填空題
13.15
14.210
15.
16.①④
三、解答題:
17. 解:(注:考試中計(jì)算此題可以使用分?jǐn)?shù),以下的解答用的是小數(shù))
(Ⅰ)同文(Ⅰ)
(Ⅱ) 的概率分別為
的概率分別為




隨機(jī)變量 的概率分布為
的概率分布為

0
1
2
3
P
0.216
0.432
0.288
0.064
………………8分
 的數(shù)學(xué)期望為E
的數(shù)學(xué)期望為E =0×0.216+1×0.432+2×0.288+3×0.064=1.2.…………10分
=0×0.216+1×0.432+2×0.288+3×0.064=1.2.…………10分
(或利用E =mp=3×0.4=1.2)
=mp=3×0.4=1.2)
 的方差為
的方差為
D =(0-1.2)2×0.216+(1-1.2)2×0.432+(2-1.2)2×0.288+(3-1.2)2×0.064
=(0-1.2)2×0.216+(1-1.2)2×0.432+(2-1.2)2×0.288+(3-1.2)2×0.064
=0.72.…………………………12分
(或利用D =nq=3×0.4×0.6=0.72)
=nq=3×0.4×0.6=0.72)
18.解:
(Ⅰ)
…………4分
所以, 的最小正周期
的最小正周期 ,最小值為-2.…………………………6分
,最小值為-2.…………………………6分
(Ⅱ)列表:
x
0





|