
題目列表(包括答案和解析)
已知函數 .
.
(Ⅰ)求函數 的單調區間;
的單調區間;
(Ⅱ)設 ,若對任意
,若對任意 ,
, ,不等式
,不等式 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.
【解析】第一問利用 的定義域是
的定義域是

由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函數 的單調遞增區間是(1,3);單調遞減區間是
的單調遞增區間是(1,3);單調遞減區間是
第二問中,若對任意 不等式
不等式 恒成立,問題等價于
恒成立,問題等價于 只需研究最值即可。
只需研究最值即可。
解: (I) 的定義域是
的定義域是 ......1分
......1分
 ............. 2分
............. 2分
由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函數 的單調遞增區間是(1,3);單調遞減區間是
的單調遞增區間是(1,3);單調遞減區間是 ........4分
........4分
(II)若對任意 不等式
不等式 恒成立,
恒成立,
問題等價于 ,
.........5分
,
.........5分
由(I)可知,在 上,x=1是函數極小值點,這個極小值是唯一的極值點,
上,x=1是函數極小值點,這個極小值是唯一的極值點,
故也是最小值點,所以 ; ............6分
; ............6分

當b<1時, ;
;
當 時,
時, ;
;
當b>2時, ;
............8分
;
............8分
問題等價于
 ........11分
........11分
解得b<1 或 或
或  即
即 ,所以實數b的取值范圍是
,所以實數b的取值范圍是
(本小題滿分12分)已知函數
(I)若函數 在區間
在區間 上存在極值,求實數a的取值范圍;
上存在極值,求實數a的取值范圍;
(II)當 時,不等式
時,不等式 恒成立,求實數k的取值范圍.
恒成立,求實數k的取值范圍.
(Ⅲ)求證:解:(1) ,其定義域為
,其定義域為 ,則
,則 令
令 ,
,
則 ,
,
當 時,
時, ;當
;當 時,
時,
 在(0,1)上單調遞增,在
在(0,1)上單調遞增,在 上單調遞減,
上單調遞減,
即當 時,函數
時,函數 取得極大值. (3分)
取得極大值. (3分)
 函數
函數 在區間
在區間 上存在極值,
上存在極值,
 ,解得
,解得 (4分)
(4分)
(2)不等式 ,即
,即
令
(6分)
令 ,則
,則 ,
,
 ,即
,即 在
在 上單調遞增, (7分)
上單調遞增, (7分)
 ,從而
,從而 ,故
,故 在
在 上單調遞增, (7分)
上單調遞增, (7分)
 (8分)
(8分)
(3)由(2)知,當 時,
時, 恒成立,即
恒成立,即 ,
,
令 ,則
,則 , (9分)
, (9分)

(10分)
以上各式相加得,

即 ,
,
即
 (12分)
(12分)
 。
。
(本題滿分12分)已知函數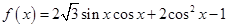
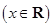 ,
,
(I)求函數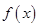 的遞增區間;
的遞增區間;
(II)求函數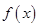 在區間
在區間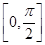 上的值域。
上的值域。
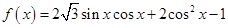
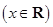 ,
,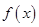 的遞增區間;
的遞增區間;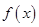 在區間
在區間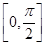 上的值域。
上的值域。
已知函數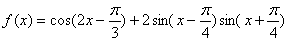
(I)求函數 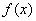 的最小正周期和圖象的對稱軸方程;
的最小正周期和圖象的對稱軸方程;
(II)求函數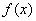 在區間
在區間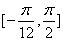 上的值域。
上的值域。
一、選擇題:
1―5 ACBBD 6―10 BCDAC
二、填空題:
11.60 12.試題.files/image132.gif) 13.―
13.―試題.files/image060.gif) 14.
14.試題.files/image135.gif)
15.2 16.試題.files/image137.gif) 17.
17.試題.files/image139.gif)
三、解答題:
18.解:(I)試題.files/image141.gif)
|