
題目列表(包括答案和解析)
(9分)已知動直線![]() 與拋物線
與拋物線![]() 相交于A點,動點B的坐標是
相交于A點,動點B的坐標是![]()
(Ⅰ)求線段AB的中點M的軌跡![]() 的方程;
的方程;
(Ⅱ)若過點N(1,0)的直線![]() 交軌跡
交軌跡![]() 于
于![]() 、
、![]() 兩點,點
兩點,點![]() 是坐標原點,若
是坐標原點,若![]() 面積為4,求直線
面積為4,求直線![]() 的傾斜角
的傾斜角![]() .
.
已知拋物線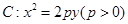 ,直線
,直線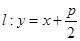 交拋物線于
交拋物線于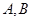 兩點,且
兩點,且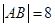 .
.
(1)求拋物線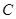 的方程;
的方程;
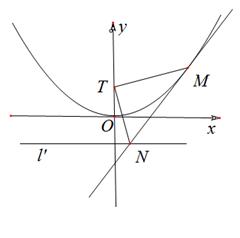
(2)若點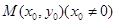 是拋物線
是拋物線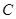 上的動點,過
上的動點,過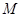 點的拋物線的切線與直線
點的拋物線的切線與直線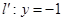 交于點
交于點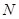 ,問在
,問在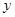 軸上是否存在定點
軸上是否存在定點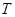 ,使得
,使得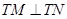 ?若存在,求出該定點,并求出
?若存在,求出該定點,并求出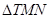 的面積的最小值;若不存在,請說明理由.
的面積的最小值;若不存在,請說明理由.
已知拋物線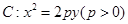 ,直線
,直線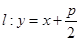 交拋物線于
交拋物線于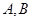 兩點,且
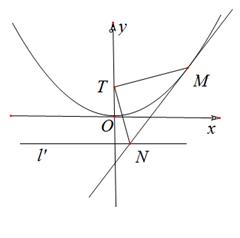
兩點,且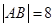 .
.
(1)求拋物線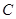 的方程;
的方程;
(2)若點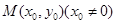 是拋物線
是拋物線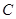 上的動點,過
上的動點,過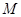 點的拋物線的切線與直線
點的拋物線的切線與直線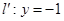 交于點
交于點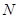 ,問在
,問在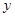 軸上是否存在定點
軸上是否存在定點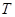 ,使得
,使得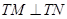 ?若存在,求出該定點,并求出
?若存在,求出該定點,并求出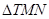 的面積的最小值;若不存在,請說明理由.
的面積的最小值;若不存在,請說明理由.
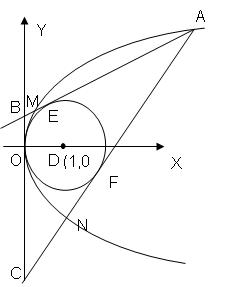
)已知,A是拋物線y2=2x上的一動點,過A作圓(x-1)2+y2=1的兩條切線分別切圓于EF兩點,交拋物線于M.N兩點,交y軸于 B.C兩點
(1)當A點坐標為(8,4)時,求直線EF的方程;
(2)當A點坐標為(2,2)時,求直線MN的方程;
(3)當A點的橫坐標大于2時,求△ABC面積的最小值。
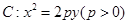 ,直線
,直線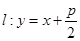 交拋物線于
交拋物線于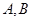 兩點,且
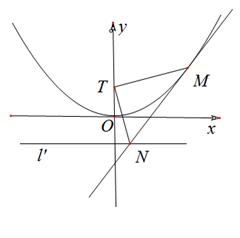
兩點,且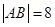 .
.
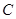 的方程;
的方程;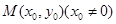 是拋物線
是拋物線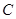 上的動點,過
上的動點,過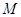 點的拋物線的切線與直線
點的拋物線的切線與直線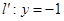 交于點
交于點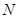 ,問在
,問在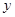 軸上是否存在定點
軸上是否存在定點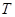 ,使得
,使得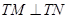 ?若存在,求出該定點,并求出
?若存在,求出該定點,并求出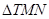 的面積的最小值;若不存在,請說明理由.
的面積的最小值;若不存在,請說明理由.1.解析: ,故選A。
,故選A。
2.解析:抽取回族學生人數是 ,故選B。
,故選B。
3.解析:由 ,得
,得 ,此時
,此時 ,所以,
,所以, ,故選C。
,故選C。
4.解析:∵ ∥
∥ ,∴
,∴ ,∴
,∴ ,故選C。
,故選C。
5.解析:設公差為 ,由題意得,
,由題意得, ;
; ,解得
,解得 或
或 ,故選C。
,故選C。
6.解析:∵雙曲線 的右焦點到一條漸近線的距離等于焦距的
的右焦點到一條漸近線的距離等于焦距的 ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ,∴雙曲線的漸近線方程是
,∴雙曲線的漸近線方程是 ,故選D.
,故選D.
7.解析:∵ 、
、 為正實數,∴
為正實數,∴ ,∴
,∴ ;由均值不等式得
;由均值不等式得 恒成立,
恒成立, ,故②不恒成立,又因為函數
,故②不恒成立,又因為函數 在
在 是增函數,∴
是增函數,∴ ,故恒成立的不等式是①③④。故選C.
,故恒成立的不等式是①③④。故選C.
8.解析:∵ ,∴
,∴ 在區間
在區間 上恒成立,即
上恒成立,即 在區間
在區間 上恒成立,∴
上恒成立,∴ ,故選D。
,故選D。
9.解析:∵

 ,∴此函數的最小正周期是
,∴此函數的最小正周期是 ,故選C。
,故選C。
10.解析:如圖,∵正三角形 的邊長為
的邊長為 ,∴
,∴ ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ,故選D。
,故選D。
11.解析:∵ 在區間
在區間 上是增函數且
上是增函數且 ,∴其反函數
,∴其反函數 在區間上
在區間上 是增函數,∴
是增函數,∴

 ,故選A
,故選A
12.解析:如圖,①當 或
或 時,圓面
時,圓面 被分成2塊,涂色方法有20種;②當
被分成2塊,涂色方法有20種;②當 或
或 時,圓面
時,圓面 被分成3塊,涂色方法有60種;
被分成3塊,涂色方法有60種;
③當 時,圓面
時,圓面 被分成4塊,涂色方法有120種,所以m的取值范圍是
被分成4塊,涂色方法有120種,所以m的取值范圍是 ,故選A。
,故選A。
13.解析:將 代入
代入 結果為
結果為 ,∴
,∴ 時,
時, 表示直線
表示直線 右側區域,反之,若
右側區域,反之,若 表示直線
表示直線 右側區域,則
右側區域,則 ,∴是充分不必要條件。
,∴是充分不必要條件。
 14.解析:∵
14.解析:∵ ,∴
,∴ 時,
時, ,又
,又 時,
時, 滿足上式,因此,
滿足上式,因此, 。
。
 15.解析:設正四面體的棱長為
15.解析:設正四面體的棱長為 ,連
,連 ,取
,取 的中點
的中點 ,連
,連 ,∵
,∵ 為
為 的中點,∴
的中點,∴ ∥
∥ ,∴
,∴ 或其補角為
或其補角為 與
與 所成角,∵
所成角,∵ ,
, ,∴
,∴ ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ,∴
,∴ 與
與 所成角的余弦值為
所成角的余弦值為 。
。
 16.解析:∵
16.解析:∵ ,∴
,∴ ,∵點
,∵點 為
為 的準線與
的準線與 軸的交點,由向量的加法法則及拋物線的對稱性可知,點
軸的交點,由向量的加法法則及拋物線的對稱性可知,點 為拋物線上關于軸對稱的兩點且做出圖形如右圖,其中
為拋物線上關于軸對稱的兩點且做出圖形如右圖,其中 為點
為點 到準線的距離,四邊形
到準線的距離,四邊形 為菱形,∴
為菱形,∴ ,∴
,∴ ,∴
,∴ ,∴
,∴ ,∴
,∴ ,∴向量
,∴向量 與
與 的夾角為
的夾角為 。
。
17.(10分)解析:(Ⅰ)由正弦定理得, ,
, ,…2分
,…2分
∴ ,
, ,………4分
,………4分
(Ⅱ)∵ ,
, ,∴
,∴ ,∴
,∴ ,………………………6分
,………………………6分
又∵ ,∴
,∴ ,∴
,∴ ,………………………8分
,………………………8分
∴ 。………………………10分
。………………………10分
18.解析:(Ⅰ)∵ ,∴
,∴ ;……………………理3文4分
;……………………理3文4分
(Ⅱ)∵三科會考不合格的概率均為 ,∴學生甲不能拿到高中畢業證的概率
,∴學生甲不能拿到高中畢業證的概率 ;……………………理6文8分
;……………………理6文8分
(Ⅲ)∵每科得A,B的概率分別為 ,∴學生甲被評為三好學生的概率為
,∴學生甲被評為三好學生的概率為 。……………………12分
。……………………12分
19.(12分)解析:(Ⅰ)∵ ,∴
,∴ ,
,
 ,
, ,……………3分
,……………3分
(Ⅱ)∵ ,∴
,∴
 ,
,
∴ ,
,

又 ,∴數列
,∴數列 自第2項起是公比為
自第2項起是公比為 的等比數列,………………………6分
的等比數列,………………………6分
∴ ,………………………8分
,………………………8分
(Ⅲ)∵ ,∴
,∴ ,………………10分
,………………10分
∴ 。………………………12分
。………………………12分
20.解析:(Ⅰ)∵ ∥
∥ ,
, ,∴
,∴ ,∵
,∵ 底面
底面 ,∴
,∴ ,∴
,∴ 平面
平面 ,∴
,∴ ,又∵
,又∵ 平面
平面 ,∴
,∴ ,∴
,∴ 平面
平面 ,∴
,∴ 。………………………4分
。………………………4分
(Ⅱ)∵ 平面
平面 ,∴
,∴ ,
, ,∴
,∴ 為二面角
為二面角 的平面角,………………………6分
的平面角,………………………6分
 ,
, ,∴
,∴ ,又∵
,又∵ 平面
平面 ,
, ,∴
,∴ ,∴二面角
,∴二面角 的正切值的大小為
的正切值的大小為 。………………………8分
。………………………8分
(Ⅲ)過點 做
做 ∥
∥ ,交
,交 于點
于點 ,∵
,∵ 平面
平面 ,∴
,∴ 為
為 在平面
在平面 內的射影,∴
內的射影,∴ 為
為 與平面
與平面 所成的角,………………………10分
所成的角,………………………10分
 ∵
∵ ,∴
,∴ ,又∵
,又∵ ∥
∥ ,∴
,∴ 和
和 與平面
與平面 所成的角相等,∴
所成的角相等,∴ 與平面
與平面 所成角的正切值為
所成角的正切值為 。………………………12分
。………………………12分
解法2:如圖建立空間直角坐標系,(Ⅰ)∵, ,∴點
,∴點 的坐標分別是
的坐標分別是 ,
, ,
,
 ,∴
,∴ ,
, ,設
,設 ,∵
,∵ 平面
平面 ,∴
,∴ ,∴
,∴ ,取
,取 ,∴
,∴ ,∴
,∴ 。………………………4分
。………………………4分
(Ⅱ)設二面角 的大小為
的大小為 ,∵平面
,∵平面 的法向量是
的法向量是 ,平面
,平面 的法向量是
的法向量是 ,∴
,∴ ,∴
,∴ ,∴二面角
,∴二面角 的正切值的大小為
的正切值的大小為 。………………………8分
。………………………8分
(Ⅲ)設 與平面
與平面 所成角的大小為
所成角的大小為 ,∵平面
,∵平面 的法向量是
的法向量是 ,
, ,∴
,∴ ,∴
,∴ ,∴
,∴ 與平面
與平面 所成角的正切值為
所成角的正切值為 。………………………12分
。………………………12分
21.解析:(Ⅰ)設拋物線方程為 ,將
,將 代入方程得
代入方程得
所以拋物線方程為 。………………………2分
。………………………2分
由題意知橢圓的焦點為 、
、 。
。
設橢圓的方程為 ,
,
∵過點 ,∴
,∴ ,解得,
,解得, ,
, ,
,
∴橢圓的方程為 。………………………5分
。………………………5分
(Ⅱ)設 的中點為
的中點為 ,
, 的方程為:
的方程為: ,
,
以 為直徑的圓交
為直徑的圓交 于
于 兩點,
兩點, 中點為
中點為 。
。
設 ,則
,則
∵
 ………………………8分
………………………8分
∴
 ………………………10分
………………………10分
當 時,
時, ,
, ,
,
此時,直線 的方程為
的方程為 。………………………12分
。………………………12分
22.(12分)解析:(Ⅰ)∵ 是偶函數,∴
是偶函數,∴ ,
,
又∵ ∴
∴ ,
, ,………………………2分
,………………………2分
由 得,
得, ,
,
∵ 時,
時, ;
; 時,
時, ;
; 時,
時, ;∴
;∴ 時,函數
時,函數 取得極大值
取得極大值 ,
, 時,函數
時,函數 取得極小值
取得極小值 。………………………5分
。………………………5分
(Ⅱ)∵ 在區間
在區間 上為增函數,∴
上為增函數,∴ 在
在 上恒成立,∴
上恒成立,∴
 且
且 在區間
在區間 上恒成立,………………………7分
上恒成立,………………………7分
∴
∴ ……………………9分
……………………9分
又∵ =
= ,∵
,∵
∴ ,∴
,∴ 的取值范圍是
的取值范圍是 。………………………12分
。………………………12分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com