
題目列表(包括答案和解析)
已知函數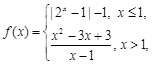 函數
函數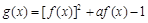 (其中a為常數),給出下列結論:
(其中a為常數),給出下列結論:
①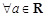 ,函數
,函數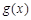 至少有一個零點;
至少有一個零點;
②當a=0時,函數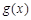 有兩個不同零點;
有兩個不同零點;
③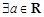 ,函數
,函數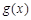 有三個不同零點;
有三個不同零點;
④函數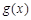 有四個不同零點的充要條件是a<0.
有四個不同零點的充要條件是a<0.
其中所有正確結論的序號是 .
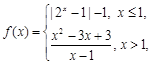 函數
函數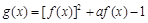 (其中a為常數),給出下列結論:
(其中a為常數),給出下列結論: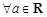 ,函數
,函數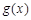 至少有一個零點;
至少有一個零點;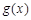 有兩個不同零點;
有兩個不同零點;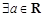 ,函數
,函數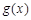 有三個不同零點;
有三個不同零點;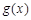 有四個不同零點的充要條件是a<0.
有四個不同零點的充要條件是a<0.已知函數f(x)=x-xlnx , ,其中
,其中 表示函數f(x)在
表示函數f(x)在
x=a處的導數,a為正常數.
(1)求g(x)的單調區間;
(2)對任意的正實數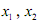 ,且
,且 ,證明:
,證明:

(3)對任意的
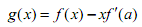 ,其中
,其中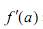 表示函數f(x)在
表示函數f(x)在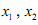 ,且
,且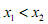 ,證明:
,證明: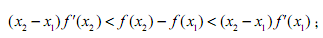
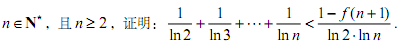
已知向量![]() =(sin2x,cos2x),
=(sin2x,cos2x),![]() =(cos
=(cos![]() ,sin
,sin![]() ),函數f(x)=
),函數f(x)=![]() +2a(其中a為實常數)
+2a(其中a為實常數)
(Ⅰ)求函數f(x)的最小正周期;(Ⅱ)求函數f(x)的單調遞減區間
一,選擇題:
D C B CC, CA BC B
二、填空題:
(11),
-3.files/image153.gif) ,
(12), 27
(13),
,
(12), 27
(13), .files/image155.gif)
(14), .files/image157.gif) . (15), -26,14,65
. (15), -26,14,65
三、解答題:
16, 由已知得.files/image159.gif) ;所以解集:
;所以解集:.files/image161.gif) ;
;
17, (1)由題意.files/image163.gif) ,
,.files/image165.gif) =1又a>0,所以a=1.
=1又a>0,所以a=1.
(2).files/image167.gif)
.files/image169.gif) g(x)=
g(x)=.files/image171.gif) ,當
,當.files/image173.gif) 時,
時,.files/image167.gif)
.files/image169.gif)
.files/image176.gif) =
=.files/image178.gif) ,無遞增區間;當x<1時,
,無遞增區間;當x<1時,.files/image167.gif)
.files/image169.gif)
.files/image176.gif) =
=.files/image180.gif) ,它的遞增區間是
,它的遞增區間是.files/image182.gif) .
.
綜上知:.files/image167.gif)
.files/image169.gif)
.files/image176.gif) 的單調遞增區間是
的單調遞增區間是.files/image182.gif) .
.
18, (1)當0<t≤10時,
.files/image185.gif) 是增函數,且f(10)=240
是增函數,且f(10)=240
當20<t≤40時,.files/image187.gif) 是減函數,且f(20)=240 所以,講課開始10分鐘,學生的注意力最集中,能持續10分鐘。(3)當0<t≤10時,令
是減函數,且f(20)=240 所以,講課開始10分鐘,學生的注意力最集中,能持續10分鐘。(3)當0<t≤10時,令.files/image189.gif) ,則t=4 當20<t≤40時,令
,則t=4 當20<t≤40時,令.files/image191.gif) ,則t≈28.57
,則t≈28.57
則學生注意力在180以上所持續的時間28.57-4=24.57>24
從而教師可以第4分鐘至第28.57分鐘這個時間段內將題講完。
19, (I).files/image193.gif) ……1分
……1分
根據題意,.files/image195.gif) …………4分
…………4分
解得.files/image197.gif) . …………7分
. …………7分
(II)因為.files/image199.gif) ……7分
……7分
(i).files/image201.gif) 時,函數
時,函數.files/image048.gif) 無最大值,
無最大值,
.files/image041.gif) 不合題意,舍去. …………11分
不合題意,舍去. …………11分
(ii).files/image204.gif) 時,根據題意得
時,根據題意得
.files/image206.gif)
解之得.files/image208.gif) …………13分
…………13分
.files/image210.gif) 為正整數,
為正整數,.files/image210.gif) =3或4. …………14分
=3或4. …………14分
20. (1)當x∈[-1,0)時, f(x)= f(-x)=loga[2-(-x)]=loga(2+x).
當x∈[2k-1,2k),(k∈Z)時,x-2k∈[-1,0], f(x)=f(x-2k)=loga[2+(x-2k)].
當x∈[2k,2k+1](k∈Z)時,x-2k∈[0,1], f(x)=f(x-2k)=loga[2-(x-2k)].
故當x∈[2k-1,2k+1](k∈Z)時, f(x)的表達式為
|