
題目列表(包括答案和解析)
(14分)已知函數![]() ,( x>0).
,( x>0).
(I)當0<a<b,且f(a)=f(b)時,求證:ab>1;
(II)是否存在實數a,b(a<b),使得函數y=f(x)的定義域、值域都是[a,b],若存在,則求出a,b的值,若不存在,請說明理由.
(III)若存在實數a,b(a<b),使得函數y=f(x)的定義域為 [a,b]時,值域為 [ma,mb]
(m≠0),求m的取值范圍.
(14分)一個袋中有8個大小相同的小球,其中紅球1個,白球和黑球若干,現從袋中有放回地取球,每次隨機取一個,又知連續取兩次都是白球的概率為1/4.
(Ⅰ)求該口袋內白球和黑球的個數;
(Ⅱ)規定取出1個紅球得2分,取出1個白色球得1分,取出1個黑色球得0分,連續取三次分數之和為4分的概率;
(Ⅲ)現甲、乙兩個小朋友做游戲,方法是:不放回從口袋中輪流摸取一個球,甲先取,乙后取,然后甲在取,直到兩個小朋友中有1人取得黑球時游戲終止,每個球在每一次被取出的機會均相同,求當游戲終止時,取球次數不多于3次的概率.
(本題14分)已知橢圓的中心在坐標原點![]() ,焦點在
,焦點在![]() 軸上,短軸長為2,且兩個焦點和短軸的兩個端點恰為一個正方形的頂點.過右焦點
軸上,短軸長為2,且兩個焦點和短軸的兩個端點恰為一個正方形的頂點.過右焦點![]() 與
與![]() 軸不垂直的直線
軸不垂直的直線![]() 交橢圓于
交橢圓于![]() ,
,![]() 兩點.
兩點.
(Ⅰ)求橢圓的方程;
(Ⅱ)當直線![]() 的斜率為1時,求
的斜率為1時,求![]() 的面積;
的面積;
(Ⅲ)在線段![]() 上是否存在點
上是否存在點![]() ,使得以
,使得以![]() 為鄰邊的平行四邊形是菱形?
為鄰邊的平行四邊形是菱形?
 若存在,求出
若存在,求出![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
(本題14分)已知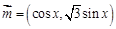 ,
,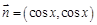 ,設
,設 .
.
(1)求函數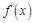 的圖像的對稱軸及其單調遞增區間;
的圖像的對稱軸及其單調遞增區間;
(2)當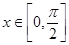 ,求函數
,求函數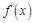 的值域及取得最大值時
的值域及取得最大值時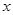 的值;
的值;
(3)若 分別是銳角
分別是銳角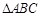 的內角
的內角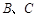 的對邊,且
的對邊,且 ,
,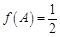 ,試求
,試求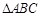 的面積
的面積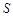 .
.
(本題14分)北京奧運會紀念章某特許專營店銷售紀念章,每枚進價為5元,同時每銷售一枚這種紀念章還需向北京奧組委交特許經營管理費2元,預計這種紀念章以每枚20元的價格銷售時該店一年可銷售2000枚,經過市場調研發現每枚紀念章的銷售價格在每枚20元的基礎上每減少一元則增加銷售400枚,而每增加一元則減少銷售100枚,現設每枚紀念章的銷售價格為![]() 元.
元.
(Ⅰ)寫出該特許專營店一年內銷售這種紀念章所獲得的利潤![]() (元)與每枚紀念章的銷售價格
(元)與每枚紀念章的銷售價格![]() 的函數關系式(并寫出這個函數的定義域);
的函數關系式(并寫出這個函數的定義域);
(Ⅱ)當每枚紀念銷售價格![]() 為多少元時,該特許專營店一年內利潤
為多少元時,該特許專營店一年內利潤![]() (元)最大,并求出這個最大值.
(元)最大,并求出這個最大值.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com