
題目列表(包括答案和解析)
在 中,
中,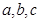 ,分別是角
,分別是角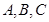 所對(duì)邊的長,
所對(duì)邊的長,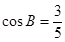 ,且
,且
(1)求 的面積;
的面積;
(2)若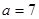 ,求角C.
,求角C.
【解析】第一問中,由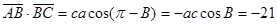 又∵
又∵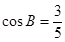 ∴
∴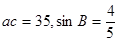 ∴
∴ 的面積為
的面積為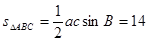
第二問中,∵a =7 ∴c=5由余弦定理得: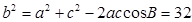 得到b的值,然后又由余弦定理得:
得到b的值,然后又由余弦定理得: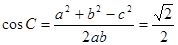
又C為內(nèi)角 ∴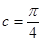
解:(1)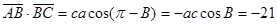 ………………2分
………………2分
又∵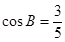 ∴
∴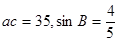 ……………………4分
……………………4分
∴ 的面積為
的面積為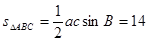 ……………………6分
……………………6分
(2)∵a =7 ∴c=5 ……………………7分
由余弦定理得: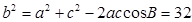
∴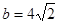 ……………………9分
……………………9分
又由余弦定理得: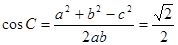
又C為內(nèi)角 ∴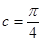 ……………………12分
……………………12分
另解:由正弦定理得: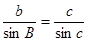 ∴
∴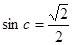 又
又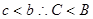 ∴
∴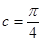
已知在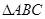 中,
中,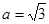 ,
,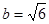 ,
,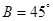 ,解這個(gè)三角形;
,解這個(gè)三角形;
【解析】本試題主要考查了正弦定理的運(yùn)用。由正弦定理得到: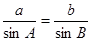
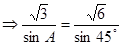 ,然后又
,然后又 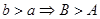
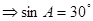
又 再又
再又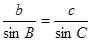 得到c。
得到c。
解:由正弦定理得到: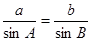
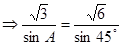
又 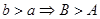
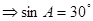 ……4分
……4分
又 ……8分
……8分
又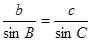
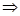
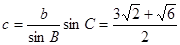
如圖,在四棱錐 中,
中, ⊥底面
⊥底面 ,底面
,底面 為正方形,
為正方形, ,
, ,
, 分別是
分別是 ,
, 的中點(diǎn).
的中點(diǎn).
(I)求證: 平面
平面 ;
;
(II)求證: ;
;
(III)設(shè)PD=AD=a, 求三棱錐B-EFC的體積.

【解析】第一問利用線面平行的判定定理, ,得到
,得到
第二問中,利用
 ,所以
,所以
又因?yàn)?img
src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012061921145879762728/SYS201206192116075476939219_ST.files/image018.png">, ,從而得
,從而得
第三問中,借助于等體積法來求解三棱錐B-EFC的體積.
(Ⅰ)證明:
 分別是
分別是 的中點(diǎn),
的中點(diǎn), 
 ,
, . …4分
. …4分
(Ⅱ)證明: 四邊形
四邊形 為正方形,
為正方形, .
.
 ,
,  .
.
 ,
,  ,
,
 .
. ,
, . ………8分
. ………8分
(Ⅲ)解:連接AC,DB相交于O,連接OF, 則OF⊥面ABCD,
∴

在四棱錐 中,
中, 平面
平面 ,底面
,底面 為矩形,
為矩形, .
.
(Ⅰ)當(dāng) 時(shí),求證:
時(shí),求證: ;
;
(Ⅱ)若 邊上有且只有一個(gè)點(diǎn)
邊上有且只有一個(gè)點(diǎn) ,使得
,使得 ,求此時(shí)二面角
,求此時(shí)二面角 的余弦值.
的余弦值.

【解析】第一位女利用線面垂直的判定定理和性質(zhì)定理得到。當(dāng)a=1時(shí),底面ABCD為正方形,

又因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912265168707359/SYS201207091227226245550949_ST.files/image014.png">, ………………2分
………………2分
又 ,得證。
,得證。
第二問,建立空間直角坐標(biāo)系,則B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)……4分
設(shè)BQ=m,則Q(1,m,0)(0《m《a》
要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 時(shí),存在點(diǎn)Q使得
時(shí),存在點(diǎn)Q使得
當(dāng)且僅當(dāng)m=a-m,即m=a/2時(shí),BC邊上有且只有一個(gè)點(diǎn)Q,使得
由此知道a=2, 設(shè)平面POQ的法向量為
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
則 的大小與二面角A-PD-Q的大小相等所以
的大小與二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值為
解:(Ⅰ)當(dāng) 時(shí),底面ABCD為正方形,
時(shí),底面ABCD為正方形,

又因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912265168707359/SYS201207091227226245550949_ST.files/image014.png">, 又
又
 ………………3分
………………3分
(Ⅱ) 因?yàn)锳B,AD,AP兩兩垂直,分別以它們所在直線為X軸、Y軸、Z軸建立坐標(biāo)系,如圖所示,

則B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)…………4分
設(shè)BQ=m,則Q(1,m,0)(0《m《a》要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 時(shí),存在點(diǎn)Q使得
時(shí),存在點(diǎn)Q使得
當(dāng)且僅當(dāng)m=a-m,即m=a/2時(shí),BC邊上有且只有一個(gè)點(diǎn)Q,使得 由此知道a=2,
由此知道a=2,
設(shè)平面POQ的法向量為
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
則 的大小與二面角A-PD-Q的大小相等所以
的大小與二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值為
已知四棱錐P-ABCD,底面ABCD是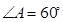 、邊長為
、邊長為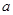 的菱形,又
的菱形,又 ,且PD=CD,點(diǎn)M、N分別是棱AD、PC的中點(diǎn).
,且PD=CD,點(diǎn)M、N分別是棱AD、PC的中點(diǎn).
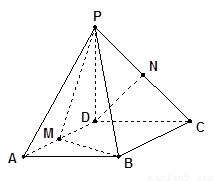
(1)證明:MB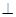 平面PAD;
平面PAD;
(2)求點(diǎn)A到平面PMB的距離.
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com