題目列表(包括答案和解析)
(本大題滿分12分)
已知點A(－1，0)、B(1，0)和動點M滿足：
，且
，動點M的軌跡為曲線C，過點B的直線交C于P、Q兩點．
(1)求曲線C的方程；
(2)求△APQ面積的最大值．
(本小題滿分12分)
已知函數f（x）=x3－ax2，其中a為實常數.
（1）設當x∈（0，1）時，函數y = f（x）圖象上任一點P處的切線的斜線率為k，若k≥－1，求a的取值范圍
（2）當x∈［－1，1］時，求函數y=f（x）+a（x2－3x）的最大值.
(本小題滿分12分)
已知函數f（x）=x3－ax2，其中a為實常數.
（1）設當x∈（0，1）時，函數y = f（x）圖象上任一點P處的切線的斜線率為k，若k≥－1，求a的取值范圍
（2）當x∈［－1，1］時，求函數y=f（x）+a（x2－3x）的最大值.
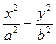=1（a＞0，b＞0）的一條準線方程為x=
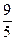，一個頂點到一條漸近線的距離為
.
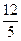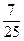，求動點P的軌跡方程.已知直三棱柱
中, 
,
，
是
和
的交點, 若
.
（1）求
的長； （2）求點
到平面
的距離；
（3）求二面角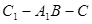
的平面角的正弦值的大小.
【解析】本試題主要考查了距離和角的求解運用。第一問中，利用ACC
A為正方形, 
AC=3
第二問中，利用面BBCC內作CD
BC,
則CD就是點C平面ABC的距離CD=
，第三問中，利用三垂線定理作二面角的平面角，然后利用直角三角形求解得到其正弦值為
解法一: (1)連AC交AC于E, 易證ACCA為正方形, AC=3
…………… 5分
(2)在面BBCC內作CDBC,
則CD就是點C平面ABC的距離CD= … 8分
(3) 易得AC面ACB,
過E作EHAB于H, 連HC,
則HCAB
CHE為二面角C－AB－C的平面角. ……… 9分
sinCHE=二面角C－AB－C的平面角的正弦大小為 ……… 12分
解法二: (1)分別以直線CB、CC、CA為x、y為軸建立空間直角坐標系, 設|CA|=h, 則C(0,
0, 0), B(4,
0, 0), B(4, －3, 0), C(0, －3,
0), A(0,
0, h), A(0, －3, h), G(2, －
, －
) ……………………… 3分
=(2, －, －), 
=(0,
－3, －h) ……… 4分
·=0,
h=3
(2)設平面ABC得法向量
=(a, b, c),則可求得=(3, 4, 0) (令a=3)
點A到平面ABC的距離為H=|
|=……… 8分
(3) 設平面ABC的法向量為
=(x, y, z),則可求得=(0, 1, 1) (令z=1)
二面角C－AB－C的大小
滿足cos=
=
………
11分
二面角C－AB－C的平面角的正弦大小為
一．選擇題：DCBBA
二．填空題：11．4x－3y－17 = 0 12．33 13．
14．
15．
三．解答題：
16．(1)解：由頻率分布條形圖知，抽取的學生總數為
人 4分
∵各班被抽取的學生人數成等差數列，設其公差為d
由4×22＋6d = 100解得：d = 2 6分
∴各班被抽取的學生人數分別是22人，24人，26人，28人． 8分
(2)解：在抽取的學生中，任取一名學生，分數不小于90分的概率為
0.35+0.25+0.1+0.05=0.75 12分
17．(1)解：∵
，
2分
∴由
得：
，即
4分
又∵
，∴
6分
(2)解：
8分
由
得：
，即
10分
兩邊平方得：
，∴
12分
18．方法一
(1)證：∵CD⊥AB，CD⊥BC，∴CD⊥平面ABC 2分
又∵CDÌ平面ACD，∴平面ACD⊥平面ABC 4分
(2)解：∵AB⊥BC，AB⊥CD，∴AB⊥平面BCD，故AB⊥BD
∴∠CBD是二面角C－AB－D的平面角
6分
∵在Rt△BCD中，BC = CD，∴∠CBD = 45°
即二面角C－AB－D的大小為45°
8分
(3)解：過點B作BH⊥AC，垂足為H，連結DH
∵平面ACD⊥平面ABC，∴BH⊥平面ACD，
∴∠BDH為BD與平面ACD所成的角
10分
設AB = a，在Rt△BHD中，
，
∴
， 10分
解得：
，即線段AB的長度為1 12分
方法二
(1)同方法一 4分
(2)解：設以過B點且∥CD的向量為x軸，
為y軸和z軸建立如圖所示的空間直角坐標系，設AB = a，則A(0，0，a)，C(0，1，0)，D(1，1，0)，
= (1，1，0)，
= (0，0，a)
平面ABC的法向量
= (1，0，0)
設平面ABD的一個法向量為n = (x，y，z)，則
取n = (1，－1，0)
6分
∴二面角C－AB－D的大小為45° 8分
(3)解：
= (0，1，－a)，
= (1，0，0)，
= (1，1，0)
設平面ACD的一個法向量是m = (x，y，z)，則
∴取m = (0，a，1)，由直線BD與平面ACD所成角為30°，故向量、m的夾角為60°
故
10分
解得：，即線段AB的長度為1 12分
19．(1)解：設M (x，y)，在△MAB中，| AB | = 2，
∴
即
2分
因此點M的軌跡是以A、B為焦點的橢圓，a = 2，c = 1
∴曲線C的方程為
． 4分
(2)解法一：設直線PQ方程為
(
∈R)
由
得：
6分
顯然，方程①的
，設P(x1，y1)，Q(x2，y2)，則有
8分
令
，則t≥4，
10分
當
時有最大值9，故
，即S≤3，∴△APQ的最大值為3 12分
解法二：設P(x1，y1)，Q(x2，y2)，則
當直線PQ的斜率不存在時，易知S = 3
設直線PQ方程為
由
得：
① 6分
顯然，方程①的△＞0，則
∴
8分
10分
令
，則
∴
，即S＜3
∴△APQ的最大值為3 12分
20．(1)解：
∵a＜0，∴
故函數f (x)在區間(－∞，
)、(－a，＋∞)上單調遞增，在(，－a)上單調遞減 4分
(2)解：∵二次函數
有最大值，∴a＜0 5分
由
得：
6分
∵函數
與
的圖象只有一個公共點，
∴
，又a＜0，∴－1≤a＜0 8分
又
，∴
(－1≤a＜0) 10分
(3)解：當a < 0時，函數f (x)在區間(－∞，)、(－a，＋∞)上單調遞增，
函數g (x)在區間(－∞，
)上單調遞增
∴
12分
當a > 0時，函數f (x)在區間(－∞，－a)、(，＋∞)上單調遞增，
函數g (x)在區間(，＋∞)上單調遞增
∴
綜上所述，實數a的取值范圍是(－∞，
]∪[3，＋∞) 13分
21．(1)解：記
令x = 1得：
令x =－1得：
兩式相減得：
，∴
4分
當n≥2時，
當n = 1時，
，適合上式
∴
6分
(2)解：
注意到
8分
可改寫為：
∴
故
10分
∴
12分
14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com