
題目列表(包括答案和解析)
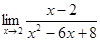 的值為
( )
的值為
( )
A.0 B.1 C.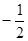 D.
D.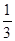
![]() 的值為
的值為
A.0 B.1 C.![]() D.
D.![]()
![]() 的值為
的值為
A.0 B.1 C.![]() D.
D.![]()
![]() 的值為 ( )
的值為 ( )
A.0 B.1 C.![]() D.
D.![]()
若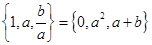 ,則
,則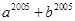 的值為
( )
的值為
( )
A.0
B.1
C.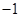 D.1或
D.1或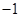
一.選擇題:DCBBA
二.填空題:11.4x-3y-17 = 0 12.33 13.
14. 15.
15.
三.解答題:
16.(1)解:∵ ,
, 2分
2分
∴由 得:
得: ,即
,即 4分
4分
又∵ ,∴
,∴ 6分
6分
(2)解: 8分
8分
由 得:
得: ,即
,即 10分
10分
兩邊平方得: ,∴
,∴ 12分
12分
 17.方法一
17.方法一
(1)證:∵CD⊥AB,CD⊥BC,∴CD⊥平面ABC 2分
又∵CDÌ平面ACD,∴平面ACD⊥平面ABC 4分
(2)解:∵AB⊥BC,AB⊥CD,∴AB⊥平面BCD,故AB⊥BD
∴∠CBD是二面角C-AB-D的平面角
6分
∵在Rt△BCD中,BC = CD,∴∠CBD = 45°
即二面角C-AB-D的大小為45°
8分
(3)解:過點B作BH⊥AC,垂足為H,連結DH
∵平面ACD⊥平面ABC,∴BH⊥平面ACD,
∴∠BDH為BD與平面ACD所成的角
10分
設AB = a,在Rt△BHD中, ,
,
∴
又 ,∴
,∴ 12分
12分
 方法二
方法二
(1)同方法一 4分
(2)解:設以過B點且∥CD的向量為x軸, 為y軸和z軸建立如圖所示的空間直角坐標系,設AB = a,則A(0,0,a),C(0,1,0),D(1,1,0),
為y軸和z軸建立如圖所示的空間直角坐標系,設AB = a,則A(0,0,a),C(0,1,0),D(1,1,0), = (1,1,0),
= (1,1,0), = (0,0,a)
= (0,0,a)
平面ABC的法向量 = (1,0,0)
= (1,0,0)
設平面ABD的一個法向量為n = (x,y,z),則

取n = (1,-1,0)
6分

∴二面角C-AB-D的大小為45° 8分
(3)解: = (0,1,-a),
= (0,1,-a), = (1,0,0),
= (1,0,0), = (1,1,0)
= (1,1,0)
設平面ACD的一個法向量是m = (x,y,z),則
∴可取m = (0,a,1),設直線BD與平面ACD所成角為 ,則向量
,則向量 、m的夾角為
、m的夾角為
故 10分
10分
即
又 ,∴
,∴ 12分
12分
18.解:該商場應在箱中至少放入x個其它顏色的球,獲得獎金數為 ,
,
則 = 0,100,150,200
= 0,100,150,200
 ,
, ,
,
 ,
, 8分
8分
∴ 的分布列為
的分布列為
|