題目列表(包括答案和解析)
已知函數
的圖像與函數
的圖像關于點
對稱
（1）求函數的解析式；
（2）若
，
在區間
上的值不小于6，求實數a的取值范圍.
已知函數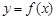
的圖像與函數
的圖像關于直線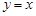
對稱，那么下列情形不可能出現的是（ ）
（A）函數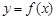有最小值
（B）函數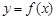過點（4，2）
（C）函數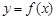是偶函數
（D）函數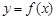在其定義域上是增函數
已知函數
的圖像與函數
的圖像關于點
對稱
（Ⅰ）求的解析式；
（Ⅱ）若
，且
在區間
上為減函數，求實數
的取值范圍.
已知函數
的圖像與函數
的圖像關于直線
對稱，記
．若
在區間
上是增函數，則實數
的取值范圍是
Ａ．
B．
Ｃ．
D．
已知函數
的圖像與函數
的圖像關于直線
對稱，則
A．
B．
C．
D．
一、選擇題1B 2D 3B 4C 5A 6D 7A 8C 9C 10D 11B 12 A
二、填空題13、 2 ； 14、 6 ；15、
16、
或 
三、解答題
17．（10分）
解：（I）
當
,即
時, 
取得最大值
.
函數的取得最大值的自變量
的集合為
…………5分
(II)
由題意得: 
即 
又由
因此函數的單調減區間為
.……10分
18.（12分）
解：（I）
…………………………4分
(II)由已知抽取一次停止的概率為
， ………………6分
抽取兩次停止的概率為
，………………………………………8分
抽取三次停止的概率為
，………………………………10分
所以抽取次數不多于三次的概率
…………12分
19.（12分） 解：（Ⅰ）取BC中點F，連結AF，則CF＝AD，且CF∥AD，
∴四邊形ADCF是平行四邊形，∴AF∥CD，
∴∠PAF（或其補角）為異面直線PA與CD所成的角 ……………………… 2分
∵PB⊥平面ABCD，∴PB⊥BA，PB⊥BF．
∵PB＝AB＝BF＝1，∴AB⊥BC，∴PA＝PF＝AF＝
．
∴△PAF是正三角形，∠PAF＝60°
即異面直線PA與CD所成的角等于60°． ……………4分
（Ⅱ）在Rt△PBD中，PB＝1，BD＝，∴PD＝
∵DE＝2PE，∴PE＝
則
，∴△PBE∽△PDB，∴BE⊥PD． …………………… 5分
由（Ⅰ）知，CF＝BF＝DF，∴∠CDB＝90°．
∴CD⊥BD．又PB⊥平面PBD，∴PB⊥CD．
∴CD⊥平面PBD，∴CD⊥BE ………………………………7分
∴BE⊥平面PCD． …………………………………………8分
（Ⅲ）連結AF，交BD于點O，則AO⊥BD．
∵PB⊥平面ABCD，∴平面PBD⊥平面ABD，∴AO⊥平面PBD．
過點O作OH⊥PD于點H，連結AH，則AH⊥PD．
∴∠AHO為二面角A－PD－B的平面角． ………………………………… 10分
在Rt△ABD中，AO＝．
在Rt△PAD中，AH＝
．
在Rt△AOH中，sin∠AHO＝
．
∴∠AHO＝60°．
即二面角A－PD－B的大小為60°． ……………………………………… 12分
20.（12分） 解：（Ⅰ）由已知
可得當
，
兩式相減得
即
，從而
當
時，
，所以 
，又
，所以 
所以有 
故總有
，
，又
從而
；………6分
（II）由（I）知
因為
=
=
-
記
，由錯位減法，可得
……………10分
故
……………12分
21.(12分) 解：（Ⅰ）
因為
點在的圖像上，
當為切點時，切線的斜率
，
此時過點的切線方程為
；……………2分
當不是切點時，若切線存在，則切線的斜率k存在，設切點為
，
……………4分
可設切線方程為
，由于切點在切線上，
①
又切點在曲線上，
②
聯立①②解得
所以另一條切線方程為
………6分
（II）由
可得
當
和
時，
，當
時，
，故的單調遞減區間為
和；單調遞增區間為
；且
……………12分
22.解：（Ⅰ）依題意，直線 AM方程為：y=k(x－2)，
|
.…………6分
時，易求直線
方程為
……8分
時，
，同理可求出N點坐標，
………………10分
，
，0）.……………………………………12分