
題目列表(包括答案和解析)
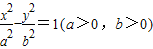 的左、右焦點,過F1垂直于x軸的直線與雙曲線交于A、B兩點,若△ABF2為銳角三角形,則雙曲線的離心率e的取值范圍是 .
的左、右焦點,過F1垂直于x軸的直線與雙曲線交于A、B兩點,若△ABF2為銳角三角形,則雙曲線的離心率e的取值范圍是 .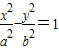 的左、右焦點,過F1且垂直于x軸的直線與雙曲線交于A、B兩點,若△ABF2為銳角三角形,則該雙曲線的離心率e的取值范圍是( )
的左、右焦點,過F1且垂直于x軸的直線與雙曲線交于A、B兩點,若△ABF2為銳角三角形,則該雙曲線的離心率e的取值范圍是( )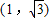

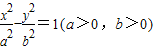 的左、右焦點,過F1垂直于x軸的直線與雙曲線交于A、B兩點,若△ABF2為銳角三角形,則雙曲線的離心率e的取值范圍是 .
的左、右焦點,過F1垂直于x軸的直線與雙曲線交于A、B兩點,若△ABF2為銳角三角形,則雙曲線的離心率e的取值范圍是 .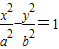 的左、右焦點,過F1且垂直于x軸的直線與雙曲線交于A、B兩點,若△ABF2為銳角三角形,則該雙曲線的離心率e的取值范圍是( )
的左、右焦點,過F1且垂直于x軸的直線與雙曲線交于A、B兩點,若△ABF2為銳角三角形,則該雙曲線的離心率e的取值范圍是( )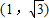
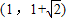
 的左、右焦點,過F1且垂直于x軸的直線與雙曲線交于A、B兩點,若△ABF2為銳角三角形,則該雙曲線的離心率e的取值范圍是( )
的左、右焦點,過F1且垂直于x軸的直線與雙曲線交于A、B兩點,若△ABF2為銳角三角形,則該雙曲線的離心率e的取值范圍是( )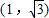
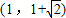
一、1―5 DDDBB 6―10 CABCA 11―12 CD
二、13.試題(全國).files/image121.gif)
14.甲 15.12,3 16.試題(全國).files/image123.gif)
三、17.解:
(1)∵試題(全國).files/image125.gif)
=試題(全國).files/image127.gif)
=試題(全國).files/image129.gif)
=試題(全國).files/image131.gif)
=試題(全國).files/image133.gif)
∴周期試題(全國).files/image135.gif)
(2)∵試題(全國).files/image137.gif)
因為試題(全國).files/image139.gif) 在區間
在區間試題(全國).files/image141.gif) 上單調遞增,
上單調遞增,
在區間試題(全國).files/image143.gif) 上單調遞減,
上單調遞減,
所以,當試題(全國).files/image145.gif) 時,
時,試題(全國).files/image094.gif) 取最大值1
取最大值1
又試題(全國).files/image148.gif)
∴當試題(全國).files/image150.gif) 時,
時,試題(全國).files/image094.gif) 取最小值
取最小值試題(全國).files/image152.gif)
所以函數試題(全國).files/image094.gif) 在區間
在區間試題(全國).files/image154.gif) 上的值域為
上的值域為試題(全國).files/image156.gif)
18.證明:
(Ⅰ)連接AC,則F是AC的中點,在△CPA中,EF∥PA…………………………3分
且PC試題(全國).files/image158.gif) 平面PAD,EF
平面PAD,EF試題(全國).files/image160.gif) PAD,
PAD,
∴EF∥平面PAD…………………………………………………………………………6分
(Ⅱ)因為平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,又CD⊥AD,
∴CD⊥平面PAD,∴CD⊥PA…………………………………………………………8分
又PA=PD=試題(全國).files/image162.gif) AD,∴△PAD是等腰直角三角形,且∠APD=
AD,∴△PAD是等腰直角三角形,且∠APD=試題(全國).files/image164.gif)
即PA⊥PD………………………………………………………………………………10分
而CD∩PD=D,∴PA⊥平面PDC,又EF∥PA,∴EF⊥平面PDC………………12分
19.(I)由試題(全國).files/image166.gif) ①
①
試題(全國).files/image168.gif) ②
②
①-②得:試題(全國).files/image170.gif)
即試題(全國).files/image172.gif)
試題(全國).files/image174.gif)
試題(全國).files/image176.gif)
試題(全國).files/image178.gif)
(II)試題(全國).files/image180.gif)
試題(全國).files/image182.gif)
試題(全國).files/image184.gif)
試題(全國).files/image186.gif)
試題(全國).files/image188.gif)
故試題(全國).files/image109.gif)
20.解:(1)試題(全國).files/image191.gif)
(2)試題(全國).files/image193.gif)
試題(全國).files/image195.gif)
由試題(全國).files/image197.gif) 及bc=20與a=3
及bc=20與a=3
解得b=4,c=5或b=5,c=4
(3)設D到三邊的距離分別為x、y、z
則試題(全國).files/image199.gif)
試題(全國).files/image201.gif)
又x、y滿足試題(全國).files/image203.gif)
畫出不等式表示的平面區域得:試題(全國).files/image205.gif)
21.解:(1)試題(全國).files/image207.gif)
由于函數試題(全國).files/image115.gif) 時取得極值,
時取得極值,
所以試題(全國).files/image210.gif)
即試題(全國).files/image212.gif)
(2)方法一
由 題設知:試題(全國).files/image214.gif)
對任意試題(全國).files/image216.gif) 都成立
都成立
即試題(全國).files/image218.gif) 對任意
對任意試題(全國).files/image216.gif) 都成立
都成立
設試題(全國).files/image220.gif) ,
,
則對任意試題(全國).files/image222.gif) 為單調遞增函數
為單調遞增函數試題(全國).files/image224.gif)
所以對任意試題(全國).files/image226.gif) 恒成立的充分必要條件是
恒成立的充分必要條件是試題(全國).files/image228.gif)
即試題(全國).files/image230.gif)
于是x的取值范圍是試題(全國).files/image232.gif)
方法二
由題設知:試題(全國).files/image214.gif)
對任意試題(全國).files/image216.gif) 都成立
都成立
即試題(全國).files/image218.gif)
對任意試題(全國).files/image216.gif) 都成立
都成立
于是試題(全國).files/image236.gif) 對任意
對任意試題(全國).files/image216.gif) 都成立,
都成立,
即試題(全國).files/image238.gif)
試題(全國).files/image240.gif)
于是x的取值范圍是試題(全國).files/image232.gif)
22.解:(I)由題意設橢圓的標準方程為試題(全國).files/image242.gif)
由已知得:試題(全國).files/image244.gif)
試題(全國).files/image246.gif)
試題(全國).files/image248.gif) 橢圓的標準方程為
橢圓的標準方程為試題(全國).files/image250.gif)
(II)設試題(全國).files/image252.gif)
聯立試題(全國).files/image254.gif)
得試題(全國).files/image256.gif)
試題(全國).files/image258.gif)
又試題(全國).files/image260.gif)
因為以AB為直徑的圓過橢圓的右焦點D(2,0)
∴試題(全國).files/image262.gif)
∴試題(全國).files/image264.gif) +
+ 試題(全國).files/image266.gif) -2
-2試題(全國).files/image268.gif)
∴試題(全國).files/image270.gif)
∴試題(全國).files/image272.gif)
解得:
試題(全國).files/image274.gif) 且均滿足
且均滿足試題(全國).files/image276.gif)
當試題(全國).files/image278.gif) ,直線過定點(2,0)與已知矛盾;
,直線過定點(2,0)與已知矛盾;
當試題(全國).files/image280.gif) 時,l的方程為
時,l的方程為試題(全國).files/image282.gif) ,直線過定點(
,直線過定點(試題(全國).files/image284.gif) ,0)
,0)
所以,直線l過定點,定點坐標為(試題(全國).files/image284.gif) ,0)
,0)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com