
題目列表(包括答案和解析)
(本小題滿分12分)![]() 學(xué)科網(wǎng)已知直四棱柱ABCD—A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F為棱BB1
學(xué)科網(wǎng)已知直四棱柱ABCD—A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F為棱BB1![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng) 的中點,M為線段AC1的中點.
的中點,M為線段AC1的中點.![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
(1)求證:直線MF∥平面ABCD;![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
(2)求證:平面AFC1⊥平面ACC1A1;![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
(3)求平面AFC1與與平面ABCD所成二面角的大小.![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
(本小題滿分12分)![]() 學(xué)科網(wǎng)已知
學(xué)科網(wǎng)已知![]() 的三邊長
的三邊長![]() 成等差數(shù)列,若點
成等差數(shù)列,若點![]() 的坐標分別為
的坐標分別為![]() .(1)求頂點
.(1)求頂點![]() 的軌跡
的軌跡![]() 的方程;
的方程;![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng) (2)若線段
(2)若線段![]() 的延長線交軌跡
的延長線交軌跡![]() 于點
于點![]() ,當
,當![]() 時求線段
時求線段![]() 的垂直平分線
的垂直平分線![]() 與
與![]() 軸交點的橫坐標的取值范圍.
軸交點的橫坐標的取值范圍.![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
(本小題滿分12分)![]() 學(xué)科網(wǎng)已知向量
學(xué)科網(wǎng)已知向量![]() ,定義函數(shù)
,定義函數(shù)![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)![]() ,求函數(shù)
,求函數(shù)![]() 的最小正周期、單調(diào)遞增區(qū)間.
的最小正周期、單調(diào)遞增區(qū)間.![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
(本小題滿分12分)![]() 學(xué)科網(wǎng)已知函數(shù)
學(xué)科網(wǎng)已知函數(shù)![]() ,
,![]() ,
,![]()
![]() 的最小值恰好是方程
的最小值恰好是方程![]() 的三個根,其中
的三個根,其中![]() .
.![]() (1)求證:
(1)求證:![]() ;
;![]() 學(xué)科網(wǎng)(2)設(shè)
學(xué)科網(wǎng)(2)設(shè)![]()
![]() 是函數(shù)
是函數(shù)![]() 的兩個極值點.若
的兩個極值點.若![]() ,
,![]() 學(xué)科網(wǎng)求函數(shù)
學(xué)科網(wǎng)求函數(shù)![]() 的解析式.
的解析式.![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
(本小題滿分12分)
已知函數(shù) ,其中,
,其中,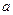 為實常數(shù)且
為實常數(shù)且
(Ⅰ)求 的單調(diào)增區(qū)間;www.www.zxxk.com[來源:學(xué),科,網(wǎng)]
的單調(diào)增區(qū)間;www.www.zxxk.com[來源:學(xué),科,網(wǎng)]
(Ⅱ)若 對任意
對任意 恒成立,求實數(shù)
恒成立,求實數(shù)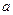 的取值范圍.
的取值范圍.
一、選擇題:本大題共10小題,每小題5分,共50分.
CBCDB DADCA
二、填空題:本大題共5小題,每小題5分,共25分.
11.90 12.[考第一次考試理科數(shù)學(xué)試卷.files/image250.gif) ) 13.
) 13.考第一次考試理科數(shù)學(xué)試卷.files/image252.gif) 14.1 ;3899 15.
14.1 ;3899 15.考第一次考試理科數(shù)學(xué)試卷.files/image254.gif)
三、解答題:本大題共6小題,共75分.
16.(本小題滿分12分)
解:(1)考第一次考試理科數(shù)學(xué)試卷.files/image133.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image157.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image256.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image258.gif) ……3分
……3分考第一次考試理科數(shù)學(xué)試卷.files/image260.gif) ……4分
……4分
令考第一次考試理科數(shù)學(xué)試卷.files/image262.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image264.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image266.gif) 的單調(diào)區(qū)間
的單調(diào)區(qū)間考第一次考試理科數(shù)學(xué)試卷.files/image268.gif) ,k∈Z ......6分
,k∈Z ......6分
(2)由考第一次考試理科數(shù)學(xué)試卷.files/image270.gif) 得
得 考第一次考試理科數(shù)學(xué)試卷.files/image272.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image274.gif) .....7分
.....7分
又考第一次考試理科數(shù)學(xué)試卷.files/image276.gif) 為
為考第一次考試理科數(shù)學(xué)試卷.files/image095.gif) 的內(nèi)角
的內(nèi)角考第一次考試理科數(shù)學(xué)試卷.files/image279.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image281.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image283.gif) ......9分
......9分
考第一次考試理科數(shù)學(xué)試卷.files/image285.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image287.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image289.gif) ...11分
...11分
考第一次考試理科數(shù)學(xué)試卷.files/image291.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image293.gif) ....12分
....12分
17. (本小題滿分12分)
解:(1)記“甲擊中目標的次數(shù)減去乙擊中目標的次數(shù)為2”為事件A,則
考第一次考試理科數(shù)學(xué)試卷.files/image295.gif) ,解得
,解得考第一次考試理科數(shù)學(xué)試卷.files/image297.gif) .....4分
.....4分
(2)考第一次考試理科數(shù)學(xué)試卷.files/image177.gif) 的所有可能取值為0,1,2.記“在第一次射擊中甲擊中目標”為事件
的所有可能取值為0,1,2.記“在第一次射擊中甲擊中目標”為事件考第一次考試理科數(shù)學(xué)試卷.files/image299.gif) ;記“在第一次射擊中乙擊中目標”為事件
;記“在第一次射擊中乙擊中目標”為事件考第一次考試理科數(shù)學(xué)試卷.files/image301.gif) .
.
則考第一次考試理科數(shù)學(xué)試卷.files/image303.gif) ,
,
考第一次考試理科數(shù)學(xué)試卷.files/image305.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image307.gif) ,.....10分
,.....10分
所以考第一次考試理科數(shù)學(xué)試卷.files/image177.gif) 的分布列為
的分布列為
考第一次考試理科數(shù)學(xué)試卷.files/image177.gif)
0
1
2
P
考第一次考試理科數(shù)學(xué)試卷.files/image311.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image171.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image314.gif)
∴考第一次考試理科數(shù)學(xué)試卷.files/image316.gif) =
=考第一次考試理科數(shù)學(xué)試卷.files/image318.gif) .....12分
.....12分考第一次考試理科數(shù)學(xué)試卷.files/image319.gif)
18. (本小題滿分12分)
解:(1)當考第一次考試理科數(shù)學(xué)試卷.files/image196.gif) 為
為考第一次考試理科數(shù)學(xué)試卷.files/image198.gif) 中點時,有
中點時,有考第一次考試理科數(shù)學(xué)試卷.files/image201.gif) 平面
平面考第一次考試理科數(shù)學(xué)試卷.files/image203.gif)
證明:連結(jié)考第一次考試理科數(shù)學(xué)試卷.files/image321.gif) 交
交考第一次考試理科數(shù)學(xué)試卷.files/image323.gif) 于
于考第一次考試理科數(shù)學(xué)試卷.files/image325.gif) ,連結(jié)
,連結(jié)考第一次考試理科數(shù)學(xué)試卷.files/image327.gif)
∵四邊形考第一次考試理科數(shù)學(xué)試卷.files/image192.gif) 是矩形 ∴
是矩形 ∴考第一次考試理科數(shù)學(xué)試卷.files/image325.gif) 為
為考第一次考試理科數(shù)學(xué)試卷.files/image321.gif) 中點
中點
又考第一次考試理科數(shù)學(xué)試卷.files/image196.gif) 為
為考第一次考試理科數(shù)學(xué)試卷.files/image198.gif) 中點,從而
中點,從而考第一次考試理科數(shù)學(xué)試卷.files/image329.gif)
∵考第一次考試理科數(shù)學(xué)試卷.files/image331.gif) 平面
平面考第一次考試理科數(shù)學(xué)試卷.files/image203.gif) ,
,考第一次考試理科數(shù)學(xué)試卷.files/image333.gif) 平面
平面考第一次考試理科數(shù)學(xué)試卷.files/image203.gif)
∴考第一次考試理科數(shù)學(xué)試卷.files/image201.gif) 平面
平面考第一次考試理科數(shù)學(xué)試卷.files/image203.gif) .....4分
.....4分
(2)建立空間直角坐標系考第一次考試理科數(shù)學(xué)試卷.files/image335.gif) 如圖所示,
如圖所示,
則考第一次考試理科數(shù)學(xué)試卷.files/image337.gif) ,
,考第一次考試理科數(shù)學(xué)試卷.files/image339.gif) ,
,考第一次考試理科數(shù)學(xué)試卷.files/image341.gif) ,
,考第一次考試理科數(shù)學(xué)試卷.files/image343.gif) ,
,考第一次考試理科數(shù)學(xué)試卷.files/image345.gif)
.....6分
所以考第一次考試理科數(shù)學(xué)試卷.files/image347.gif) ,
,考第一次考試理科數(shù)學(xué)試卷.files/image349.gif) .
.
設(shè)考第一次考試理科數(shù)學(xué)試卷.files/image351.gif) 為平面
為平面考第一次考試理科數(shù)學(xué)試卷.files/image203.gif) 的法向量,則有
的法向量,則有考第一次考試理科數(shù)學(xué)試卷.files/image353.gif) ,即
,即考第一次考試理科數(shù)學(xué)試卷.files/image355.gif)
令考第一次考試理科數(shù)學(xué)試卷.files/image357.gif) ,可得平面
,可得平面考第一次考試理科數(shù)學(xué)試卷.files/image203.gif) 的一個法向量為
的一個法向量為考第一次考試理科數(shù)學(xué)試卷.files/image359.gif) ,.....9分
,.....9分
而平面考第一次考試理科數(shù)學(xué)試卷.files/image361.gif) 的一個法向量為
的一個法向量為考第一次考試理科數(shù)學(xué)試卷.files/image363.gif) .....10分
.....10分
所以考第一次考試理科數(shù)學(xué)試卷.files/image365.gif)
所以二面角考第一次考試理科數(shù)學(xué)試卷.files/image206.gif) 的余弦值為
的余弦值為考第一次考試理科數(shù)學(xué)試卷.files/image367.gif) .....12分
.....12分
(用其它方法解題酌情給分)
19.(本小題滿分13分)
解:(1)由題意知考第一次考試理科數(shù)學(xué)試卷.files/image369.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image371.gif)
因此數(shù)列考第一次考試理科數(shù)學(xué)試卷.files/image208.gif) 是一個首項
是一個首項考第一次考試理科數(shù)學(xué)試卷.files/image374.gif) .公比為3的等比數(shù)列,所以
.公比為3的等比數(shù)列,所以考第一次考試理科數(shù)學(xué)試卷.files/image376.gif) ......2分
......2分
考第一次考試理科數(shù)學(xué)試卷.files/image378.gif) 又
又考第一次考試理科數(shù)學(xué)試卷.files/image380.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image382.gif) =100―(1+3+9)
=100―(1+3+9)
所以考第一次考試理科數(shù)學(xué)試卷.files/image384.gif) =87,解得
=87,解得考第一次考試理科數(shù)學(xué)試卷.files/image386.gif)
因此數(shù)列考第一次考試理科數(shù)學(xué)試卷.files/image210.gif) 是一個首項
是一個首項考第一次考試理科數(shù)學(xué)試卷.files/image389.gif) ,公差為―5的等差數(shù)列,
,公差為―5的等差數(shù)列,
所以 考第一次考試理科數(shù)學(xué)試卷.files/image391.gif) .....4分
.....4分
(2) 求視力不小于5.0的學(xué)生人數(shù)為考第一次考試理科數(shù)學(xué)試卷.files/image393.gif) .....7分
.....7分
(3) 由考第一次考試理科數(shù)學(xué)試卷.files/image395.gif) ①
①
可知,當考第一次考試理科數(shù)學(xué)試卷.files/image397.gif) 時,
時,考第一次考試理科數(shù)學(xué)試卷.files/image399.gif) ②
②
①-②得,當考第一次考試理科數(shù)學(xué)試卷.files/image397.gif) 時,
時,考第一次考試理科數(shù)學(xué)試卷.files/image401.gif) ,
,
考第一次考試理科數(shù)學(xué)試卷.files/image403.gif) , .....11分
, .....11分
又考第一次考試理科數(shù)學(xué)試卷.files/image405.gif)
因此數(shù)列考第一次考試理科數(shù)學(xué)試卷.files/image217.gif) 是一個從第2項開始的公比為3的等比數(shù)列,
是一個從第2項開始的公比為3的等比數(shù)列,
數(shù)列考第一次考試理科數(shù)學(xué)試卷.files/image217.gif) 的通項公式為
的通項公式為考第一次考試理科數(shù)學(xué)試卷.files/image408.gif) .....13分
.....13分
20.(本小題滿分13分)
解:(1)由于考第一次考試理科數(shù)學(xué)試卷.files/image224.gif) ,
,
∴考第一次考試理科數(shù)學(xué)試卷.files/image410.gif) ,解得
,解得考第一次考試理科數(shù)學(xué)試卷.files/image412.gif) ,
,
∴橢圓的方程是考第一次考試理科數(shù)學(xué)試卷.files/image414.gif) .....3分
.....3分
(2)∵考第一次考試理科數(shù)學(xué)試卷.files/image226.gif) ,∴
,∴考第一次考試理科數(shù)學(xué)試卷.files/image416.gif) 三點共線,
三點共線,
而考第一次考試理科數(shù)學(xué)試卷.files/image418.gif) ,設(shè)直線的方程為
,設(shè)直線的方程為考第一次考試理科數(shù)學(xué)試卷.files/image420.gif) ,
,
由考第一次考試理科數(shù)學(xué)試卷.files/image422.gif) 消去
消去考第一次考試理科數(shù)學(xué)試卷.files/image015.gif) 得:
得: 考第一次考試理科數(shù)學(xué)試卷.files/image425.gif)
由考第一次考試理科數(shù)學(xué)試卷.files/image427.gif) ,解得
,解得考第一次考試理科數(shù)學(xué)試卷.files/image429.gif) .....6分
.....6分
設(shè)考第一次考試理科數(shù)學(xué)試卷.files/image431.gif) ,由韋達定理得
,由韋達定理得考第一次考試理科數(shù)學(xué)試卷.files/image433.gif) ①,
①,
又由考第一次考試理科數(shù)學(xué)試卷.files/image226.gif) 得:
得:考第一次考試理科數(shù)學(xué)試卷.files/image435.gif) ,∴
,∴考第一次考試理科數(shù)學(xué)試卷.files/image437.gif) ②.
②.
將②式代入①式得:考第一次考試理科數(shù)學(xué)試卷.files/image439.gif) ,
,
消去考第一次考試理科數(shù)學(xué)試卷.files/image441.gif) 得:
得:考第一次考試理科數(shù)學(xué)試卷.files/image443.gif) .....10分
.....10分
設(shè)考第一次考試理科數(shù)學(xué)試卷.files/image445.gif) ,當
,當考第一次考試理科數(shù)學(xué)試卷.files/image228.gif) 時,
時, 考第一次考試理科數(shù)學(xué)試卷.files/image447.gif) 是減函數(shù),
是減函數(shù),
∴考第一次考試理科數(shù)學(xué)試卷.files/image449.gif) , ∴
, ∴考第一次考試理科數(shù)學(xué)試卷.files/image451.gif) ,
,
解得考第一次考試理科數(shù)學(xué)試卷.files/image453.gif) ,又由
,又由考第一次考試理科數(shù)學(xué)試卷.files/image429.gif) 得
得考第一次考試理科數(shù)學(xué)試卷.files/image455.gif) ,
,
∴直線AB的斜率的取值范圍是考第一次考試理科數(shù)學(xué)試卷.files/image457.gif) .....13分
.....13分
21. (本小題滿分13分)
(1)解:考第一次考試理科數(shù)學(xué)試卷.files/image459.gif)
①若考第一次考試理科數(shù)學(xué)試卷.files/image461.gif)
∵考第一次考試理科數(shù)學(xué)試卷.files/image129.gif) ,則
,則考第一次考試理科數(shù)學(xué)試卷.files/image464.gif) ,∴
,∴考第一次考試理科數(shù)學(xué)試卷.files/image466.gif) ,即
,即考第一次考試理科數(shù)學(xué)試卷.files/image468.gif) .
.
∴考第一次考試理科數(shù)學(xué)試卷.files/image133.gif) 在區(qū)間
在區(qū)間考第一次考試理科數(shù)學(xué)試卷.files/image235.gif) 是增函數(shù),故
是增函數(shù),故考第一次考試理科數(shù)學(xué)試卷.files/image133.gif) 在區(qū)間
在區(qū)間考第一次考試理科數(shù)學(xué)試卷.files/image235.gif) 的最小值是
的最小值是考第一次考試理科數(shù)學(xué)試卷.files/image470.gif)
.....2分
②若考第一次考試理科數(shù)學(xué)試卷.files/image472.gif)
令考第一次考試理科數(shù)學(xué)試卷.files/image474.gif) ,得
,得考第一次考試理科數(shù)學(xué)試卷.files/image476.gif) .
.
又當考第一次考試理科數(shù)學(xué)試卷.files/image478.gif) 時,
時,考第一次考試理科數(shù)學(xué)試卷.files/image480.gif) ;當
;當考第一次考試理科數(shù)學(xué)試卷.files/image482.gif) 時,
時,考第一次考試理科數(shù)學(xué)試卷.files/image484.gif) ,
,
∴考第一次考試理科數(shù)學(xué)試卷.files/image133.gif) 在區(qū)間
在區(qū)間考第一次考試理科數(shù)學(xué)試卷.files/image235.gif) 的最小值是
的最小值是考第一次考試理科數(shù)學(xué)試卷.files/image486.gif) .....4分
.....4分
(2)證明:當考第一次考試理科數(shù)學(xué)試卷.files/image488.gif) 時,
時,考第一次考試理科數(shù)學(xué)試卷.files/image490.gif) ,則
,則考第一次考試理科數(shù)學(xué)試卷.files/image492.gif) ,
,
∴考第一次考試理科數(shù)學(xué)試卷.files/image494.gif) ,
,
當考第一次考試理科數(shù)學(xué)試卷.files/image242.gif) 時,有
時,有考第一次考試理科數(shù)學(xué)試卷.files/image496.gif) ,∴
,∴考第一次考試理科數(shù)學(xué)試卷.files/image498.gif) 在
在考第一次考試理科數(shù)學(xué)試卷.files/image235.gif) 內(nèi)是增函數(shù),
內(nèi)是增函數(shù),
∴考第一次考試理科數(shù)學(xué)試卷.files/image501.gif) ,
,
∴考第一次考試理科數(shù)學(xué)試卷.files/image239.gif) 在
在考第一次考試理科數(shù)學(xué)試卷.files/image235.gif) 內(nèi)是增函數(shù),
內(nèi)是增函數(shù),
∴對于任意的考第一次考試理科數(shù)學(xué)試卷.files/image242.gif) ,
,考第一次考試理科數(shù)學(xué)試卷.files/image504.gif) 恒成立.....7分
恒成立.....7分
(3)證明:考第一次考試理科數(shù)學(xué)試卷.files/image506.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image508.gif) ,
,
令考第一次考試理科數(shù)學(xué)試卷.files/image510.gif)
則當考第一次考試理科數(shù)學(xué)試卷.files/image244.gif) 時,
時,考第一次考試理科數(shù)學(xué)試卷.files/image512.gif) ≥
≥考第一次考試理科數(shù)學(xué)試卷.files/image514.gif)
考第一次考試理科數(shù)學(xué)試卷.files/image516.gif) ,.....10分
,.....10分
令考第一次考試理科數(shù)學(xué)試卷.files/image518.gif) ,則
,則考第一次考試理科數(shù)學(xué)試卷.files/image520.gif) ,
,
當考第一次考試理科數(shù)學(xué)試卷.files/image522.gif) 時,
時, 考第一次考試理科數(shù)學(xué)試卷.files/image524.gif) ;當
;當考第一次考試理科數(shù)學(xué)試卷.files/image526.gif) 時,
時,考第一次考試理科數(shù)學(xué)試卷.files/image528.gif) ;當
;當考第一次考試理科數(shù)學(xué)試卷.files/image530.gif) 時,
時,考第一次考試理科數(shù)學(xué)試卷.files/image532.gif) ,
,
則考第一次考試理科數(shù)學(xué)試卷.files/image518.gif) 在
在考第一次考試理科數(shù)學(xué)試卷.files/image534.gif) 是減函數(shù),在
是減函數(shù),在考第一次考試理科數(shù)學(xué)試卷.files/image536.gif) 是增函數(shù),
是增函數(shù),
∴考第一次考試理科數(shù)學(xué)試卷.files/image538.gif) ,
,
∴考第一次考試理科數(shù)學(xué)試卷.files/image540.gif) ,
,
∴考第一次考試理科數(shù)學(xué)試卷.files/image542.gif) ,即不等式
,即不等式考第一次考試理科數(shù)學(xué)試卷.files/image133.gif) ≥
≥考第一次考試理科數(shù)學(xué)試卷.files/image239.gif) 對于任意的
對于任意的考第一次考試理科數(shù)學(xué)試卷.files/image248.gif) 恒成立.....13分
恒成立.....13分
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com