
題目列表(包括答案和解析)
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 2n+3 |
| 2n-1 |
| a | ||||||||
(1+
|
| 1 | ||
|
| Tn+2 | 2n |
已知三個(gè)正整數(shù)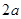 ,1,
,1, 按某種順序排列成等差數(shù)列.
按某種順序排列成等差數(shù)列.
(1)求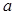 的值;
的值;
(2)若等差數(shù)列 的首項(xiàng)、公差都為
的首項(xiàng)、公差都為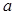 ,等比數(shù)列
,等比數(shù)列 的首項(xiàng)、公比也都為
的首項(xiàng)、公比也都為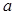 ,前
,前 項(xiàng)和分別
項(xiàng)和分別
為 ,且
,且 ,求滿足條件的正整數(shù)
,求滿足條件的正整數(shù) 的最大值.
的最大值.
已知三個(gè)正整數(shù) 按某種順序排列成等差數(shù)列。
按某種順序排列成等差數(shù)列。
(1)求 的值;
的值;
(2)若等差數(shù)列 的首項(xiàng)、公差都為
的首項(xiàng)、公差都為 ,等比數(shù)列
,等比數(shù)列 的首項(xiàng)、公比也都為
的首項(xiàng)、公比也都為 ,前
,前 項(xiàng)和分別為
項(xiàng)和分別為 ,且
,且 ,求滿足條件的正整數(shù)
,求滿足條件的正整數(shù) 的最大值。
的最大值。
已知三個(gè)正整數(shù) ,1,
,1, 按某種順序排列成等差數(shù)列.
按某種順序排列成等差數(shù)列.
(1)求 的值;
的值;
(2)若等差數(shù)列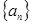 的首項(xiàng)、公差都為
的首項(xiàng)、公差都為 ,等比數(shù)列
,等比數(shù)列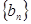 的首項(xiàng)、公比也都為
的首項(xiàng)、公比也都為 ,前
,前 項(xiàng)和分別
項(xiàng)和分別
為 ,且
,且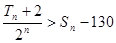 ,求滿足條件的正整數(shù)
,求滿足條件的正整數(shù) 的最大值.
的最大值.
一、選擇題:本題考查基本知識(shí)和基本運(yùn)算,每小題5分,滿分60分.
(1)A (2)B (3)D (4)C (5)A (6)B
(7)C (8)A (9)D (10)C (11)B (12)A
二、填空題:本題考查基本知識(shí)和基本運(yùn)算,每小題4分,滿分16分.
(13)校招生全國統(tǒng)一考試(江蘇卷).files\image087.png) (14)
(14)校招生全國統(tǒng)一考試(江蘇卷).files\image089.png)
(15)2
(16)校招生全國統(tǒng)一考試(江蘇卷).files\image091.png)
三、解答題
(17)本小題主要考查三角函數(shù)的基本公式和三角函數(shù)的恒等變換等基本知識(shí),以及推理能力和運(yùn)算能力.滿分12分.
解:由已知校招生全國統(tǒng)一考試(江蘇卷).files\image093.png) .
.
校招生全國統(tǒng)一考試(江蘇卷).files\image095.png)
從而 校招生全國統(tǒng)一考試(江蘇卷).files\image097.png)
校招生全國統(tǒng)一考試(江蘇卷).files\image099.png) .
.
(18)本小題主要考查線面關(guān)系和正方體性質(zhì)等基本知識(shí),考查空間想象能力和推理論證能力.滿分12分.
解法一:(I)連結(jié)BP.
∵AB⊥平面BCC1B1, ∴AP與平面BCC1B1所成的角就是∠APB,
∵CC1=4CP,CC1=4,∴CP=I.
在Rt△PBC中,∠PCB為直角,BC=4,CP=1,故BP=校招生全國統(tǒng)一考試(江蘇卷).files\image101.png) .
.
在Rt△APB中,∠ABP為直角,tan∠APB=校招生全國統(tǒng)一考試(江蘇卷).files\image103.png)
∴∠APB=校招生全國統(tǒng)一考試(江蘇卷).files\image105.png)
(19)本小題主要考查簡單線性規(guī)劃的基本知識(shí),以及運(yùn)用數(shù)學(xué)知識(shí)解決實(shí)際問題的能力.滿分12分.
解:設(shè)投資人分別用x萬元、y萬元投資甲、乙兩個(gè)項(xiàng)目.
由題意知校招生全國統(tǒng)一考試(江蘇卷).files\image107.png)
目標(biāo)函數(shù)z=x+0.5y.
上述不等式組表示的平面區(qū)域如圖所示,陰影部分(含邊界)即可行域.
|