
題目列表(包括答案和解析)
(本小題滿分14分)設橢圓 與拋物線
與拋物線 的焦點均在
的焦點均在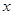 軸上,
軸上, 的中心和
的中心和 的頂點均為原點,從每條曲線上至少取兩個點,將其坐標記錄于下表中:
的頂點均為原點,從每條曲線上至少取兩個點,將其坐標記錄于下表中:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1)求 ,
, 的標準方程, 并分別求出它們的離心率
的標準方程, 并分別求出它們的離心率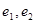 ;
;
2)設直線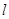 與橢圓
與橢圓 交于不同的兩點
交于不同的兩點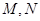 ,且
,且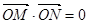 (其中
(其中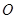 坐標原點),請問是否存在這樣的直線
坐標原點),請問是否存在這樣的直線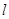 過拋物線
過拋物線 的焦點
的焦點 若存在,求出直線
若存在,求出直線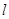 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
(本小題滿分14分)設橢圓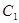 與拋物線
與拋物線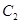 的焦點均在
的焦點均在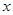 軸上,
軸上,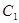 的中心和
的中心和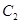 的頂點均為原點,從每條曲線上至少取兩個點,將其坐標記錄于下表中:
的頂點均為原點,從每條曲線上至少取兩個點,將其坐標記錄于下表中:
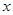 |  |  |  |  |  |
 |  |  |  |  |  |
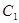 ,
,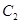 的標準方程, 并分別求出它們的離心率
的標準方程, 并分別求出它們的離心率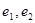 ;
; 與橢圓
與橢圓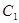 交于不同的兩點
交于不同的兩點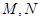 ,且
,且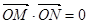 (其中
(其中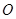 坐標原點),請問是否存在這樣的直線
坐標原點),請問是否存在這樣的直線 過拋物線
過拋物線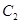 的焦點
的焦點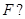 若存在,求出直線
若存在,求出直線 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.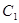 與拋物線
與拋物線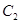 的焦點均在
的焦點均在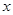 軸上,
軸上,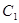 的中心和
的中心和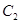 的頂點均為原點,從每條曲線上至少取兩個點,將其坐標記錄于下表中:
的頂點均為原點,從每條曲線上至少取兩個點,將其坐標記錄于下表中: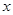 |  |  |  |  | 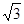 |
 |  |  |  |  |  |
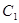 ,
,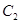 的標準方程, 并分別求出它們的離心率
的標準方程, 并分別求出它們的離心率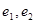 ;
;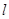 與橢圓
與橢圓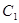 交于不同的兩點
交于不同的兩點 ,且
,且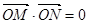 (其中
(其中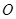 坐標原點),請問是否存在這樣的直線
坐標原點),請問是否存在這樣的直線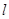 過拋物線
過拋物線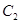 的焦點
的焦點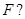 若存在,求出直線
若存在,求出直線 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.(本小題滿分14分)已知![]() 拋物線
拋物線![]()
(1)設![]() 是C1的任意兩條互相垂直的切線,并設
是C1的任意兩條互相垂直的切線,并設![]() ,證明
,證明![]() :點M的縱坐標為定值;
:點M的縱坐標為定值;![]()
(2)在C1上是否存在點P,使得C1在點P處切線與C2相交于兩點A、B,且AB的中垂線恰為C1的切線?若存在,求出點P的坐標;若不存在,說明理由。
(本小題滿分14分)某城市自西向東和自南向北的兩條主干道的東南方位有一塊空地市規劃部門計劃利用它建設一個供市民休閑健身的小型綠化廣場,如下圖所示是步行小道設計方案示意圖,

其中, 分別表示自西向東,自南向北的兩條主干道.設計方案是自主干道交匯點
分別表示自西向東,自南向北的兩條主干道.設計方案是自主干道交匯點 處修一條步行小道,小道為拋物線
處修一條步行小道,小道為拋物線 的一段,在小道上依次以點
的一段,在小道上依次以點
 為圓心,修一系列圓型小道,這些圓型小道與主干道
為圓心,修一系列圓型小道,這些圓型小道與主干道 相切,且任意相鄰的兩圓彼此外切,若
相切,且任意相鄰的兩圓彼此外切,若 (單位:百米)且
(單位:百米)且 .
.
(1)記以 為圓心的圓與主干道
為圓心的圓與主干道 切于
切于 點,證明:數列
點,證明:數列 是等差數列,并求
是等差數列,并求 關于
關于 的表達式;
的表達式;
(2)記 的面積為
的面積為 ,根據以往施工經驗可知,面積為
,根據以往施工經驗可知,面積為 的圓型小道的施工工時為
的圓型小道的施工工時為 (單位:周).試問5周時間內能否完成前
(單位:周).試問5周時間內能否完成前 個圓型小道的修建?請說明你的理由.
個圓型小道的修建?請說明你的理由.
一、DBBCA,CCBCD,BA
二、13、3,14、,15、x+y-2=0,16、12
三、解答題:
17.解:∵……………2分 ………4分
…………………………………………6分
……………………………8分
………………………………………………10分
又 ∴………………………12分
18.解:(Ⅰ)記甲、乙、丙三臺機器在一小時需要照顧分別為事件A、B、C,……1分
則A、B、C相互獨立,
由題意得: P(AB)=P(A)?P(B)=0.05
P(AC)=P(A)?P(C)=0.1
P(BC)=P(B)?P(C)=0.125…………………………………………………………4分
解得:P(A)=0.2;P(B)=0.25;P(C)=0.5
所以, 甲、乙、丙每臺機器在這個小時內需要照顧的概率分別是0.2、0.25、0.5……6分
(Ⅱ)∵A、B、C相互獨立,∴相互獨立,……………………………………7分
∴甲、乙、丙每臺機器在這個小時內需都不需要照顧的概率為
…………………………10分
∴這個小時內至少有一臺需要照顧的概率為
……12分
19.證明:(Ⅰ)作AD的中點O,則VO⊥底面
ABCD.…………………………1分
建立如圖空間直角坐標系,并設正方形邊長為1,…………………………2分
則A(,0,0),B(,1,0),C(-,1,0),D(-,0,0),V(0,0,),
∴………………………………3分
由……………………………………4分
……………………………………5分
又AB∩AV=A ∴AB⊥平面VAD…………………………………………6分
(Ⅱ)由(Ⅰ)得是面VAD的法向量………………………………7分
設是面VDB的法向量,則
……9分
∴,……………………………………11分
又由題意知,面VAD與面VDB所成的二面角,所以其大小為…………12分
20.解:由題意得:……………1分 即…………3分
又…………4分 又成等比數列,
∴該數列的公比為,………6分 所以………8分
又……………………………………10分
所以數列的通項為……………………………12分
21.解:設容器的高為x,容器的體積為V,……………………………………………1分
則V=(90-2x)(48-2x)x,(0<V<24)………………………………………………5分
=4x3-276x2+4320x ∵V′=12 x2-552x+4320………………………………7分
由V′=12 x2-552x+4320=0得x1=10,x2=36
∵x<10 時,V′>0, 10<x<36時,V′<0, x>36時,V′>0,
所以,當x=10,V有極大值V(10)=1960………………………………………10分
又V(0)=0,V(24)=0,………………………………………………………………11分
所以當x=10,V有最大值V(10)=1960……………………………………………12分
22.解:(Ⅰ)∵拋物線,即,
∴焦點為………………………………………………………1分
(1)直線的斜率不存在時,顯然有………………………………3分
(2)直線的斜率存在時,設為k, 截距為b
即直線:y=kx+b 由已知得:
……………5分
……………7分
即的斜率存在時,不可能經過焦點……………………………………8分
所以當且僅當=0時,直線經過拋物線的焦點F…………………………9分
(Ⅱ)當時,
直線的斜率顯然存在,設為:y=kx+b………………………………10分
則由(Ⅰ)得:
………………………11分
…………………………………………13分
所以直線的方程為,即………………14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com