題目列表(包括答案和解析)
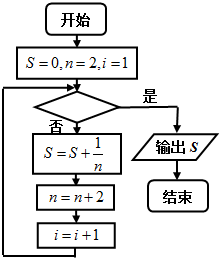，如圖給出的是計算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |
| 3 | 2 |
| an+1 |
| 4 |
| an |
| 4 |
例10 為促進個人住房商品化的進程，我國1999年元月公布了個人住房公積金貸款利率和商業性貸款利率如下：
貸款期(年數)
公積金貸款月利率(‰)
商業性貸款月利率(‰)
……
11
12
13
14
15
……
……
4.365
4.455
4.545
4.635
4.725
……
……
5.025
5.025
5.025
5.025
5.025
……
汪先生家要購買一套商品房，計劃貸款25萬元，其中公積金貸款10萬元，分十二年還清；商業貸款15萬元，分十五年還清．每種貸款分別按月等額還款，問：
(1)汪先生家每月應還款多少元?
(2)在第十二年底汪先生家還清了公積金貸款，如果他想把余下的商業貸款也一次性還清；那么他家在這個月的還款總數是多少?
(參考數據：1.004455144＝1.8966，1.005025144＝2.0581，1.005025180＝2.4651)
講解 設月利率為r，每月還款數為a元，總貸款數為A元，還款期限為n月
第1月末欠款數 A(1＋r)－a
第2月末欠款數 [A(1＋r)－a](1＋r)－a＝ A(1＋r)2－a (1＋r)－a
第3月末欠款數 [A(1＋r)2－a (1＋r)－a](1＋r)－a
＝A(1＋r)3－a (1＋r)2－a(1＋r)－a
……
第n月末欠款數 
得：
對于12年期的10萬元貸款，n＝144，r＝4.455‰
∴
對于15年期的15萬元貸款，n＝180，r＝5.025‰
∴
由此可知，
(2)至12年末，
其中A＝150000，a＝1268.22，r＝5.025‰ ∴X＝41669.53
再加上當月的計劃還款數2210.59元，當月共還款43880.12元．
需要提及的是，本題的計算如果不許用計算器，就要用到二項展開式進行估算，這在2002年全國高考第（12）題中得到考查.
例11 醫學上為研究傳染病傳播中病毒細胞的發展規律及其預防，將病毒細胞注入一只小白鼠體內進行實驗，經檢測，病毒細胞的增長數與天數的關系記錄如下表. 已知該種病毒細胞在小白鼠體內的個數超過108的時候小白鼠將死亡．但注射某種藥物，將可殺死其體內該病毒細胞的98%．
（1）為了使小白鼠在實驗過程中不死亡，第一次最遲應在何時注射該種藥物？（精確到天）
（2）第二次最遲應在何時注射該種藥物，才能維持小白鼠的生命？（精確到天）
|
, 則由
n
27.5,
,
,
，
+［g(0)- 
(p≥0),其中，g(0)是湖水污染的初始質量分數.
-［g(0)- 
=［g(0)- 
,
>e
,
,設經過t天能使湖水污染下降到初始污染水平5%即g(t)=5% g(0)?
=e
ln20，