
題目列表(包括答案和解析)
下面給出了關(guān)于復(fù)數(shù)的四種類比推理:
①復(fù)數(shù)的加減法運算可以類比多項式的加減法運算法則;
②由向量 的性質(zhì)
的性質(zhì) 類比得到復(fù)數(shù)
類比得到復(fù)數(shù) 的性質(zhì)
的性質(zhì) ;
;
③方程 有兩個不同實數(shù)根的條件是
有兩個不同實數(shù)根的條件是 可以類比得到:方程
可以類比得到:方程 有兩個不同復(fù)數(shù)根的條件是
有兩個不同復(fù)數(shù)根的條件是 ;
;
④由向量加法的幾何意義可以類比得到復(fù)數(shù)加法的幾何意義
其中類比得到的結(jié)論錯誤的是
A.①③ B.②④ C.②③ D.①④
下面給出了關(guān)于復(fù)數(shù)的四種類比推理:
①復(fù)數(shù)的加減法運算可以類比多項式的加減法運算法則;
②由向量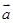 的性質(zhì)
的性質(zhì)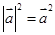 類比得到復(fù)數(shù)
類比得到復(fù)數(shù)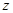 的性質(zhì)
的性質(zhì)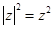 ;
;
③方程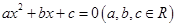 有兩個不同實數(shù)根的條件是
有兩個不同實數(shù)根的條件是 可以類比得到:方程
可以類比得到:方程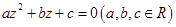 有兩個不同復(fù)數(shù)根的條件是
有兩個不同復(fù)數(shù)根的條件是 ;
;
④由向量加法的幾何意義可以類比得到復(fù)數(shù)加法的幾何意義
其中類比得到的結(jié)論錯誤的是
| A.①③ | B.②④ | C.②③ | D.①④ |
 的性質(zhì)
的性質(zhì) 類比得到復(fù)數(shù)
類比得到復(fù)數(shù) 的性質(zhì)
的性質(zhì) ;
; 有兩個不同實數(shù)根的條件是
有兩個不同實數(shù)根的條件是 可以類比得到:方程
可以類比得到:方程 有兩個不同復(fù)數(shù)根的條件是
有兩個不同復(fù)數(shù)根的條件是 ;
;| A.①③ | B.②④ | C.②③ | D.①④ |
.面給出了關(guān)于復(fù)數(shù)的四種類比推理:
①復(fù)數(shù)的加減法運算可以類比多項式的加減法運算法則;
②由向量a的性質(zhì)|a|2=a2類比得到復(fù)數(shù)z的性質(zhì)|z|2=z2;
③方程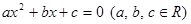 有兩個不同實數(shù)根的條件是
有兩個不同實數(shù)根的條件是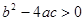 可以類比得到:方程
可以類比得到:方程 有兩個不同復(fù)數(shù)根的條件是
有兩個不同復(fù)數(shù)根的條件是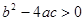 ;
;
④由向量加法的幾何意義可以類比得到復(fù)數(shù)加法的幾何意義.
其中類比錯誤的是 ( )
A.①③ B. ②④ C. ①④ D. ②③
.面給出了關(guān)于復(fù)數(shù)的四種類比推理:
①復(fù)數(shù)的加減法運算可以類比多項式的加減法運算法則;
②由向量a的性質(zhì)|a|2=a2類比得到復(fù)數(shù)z的性質(zhì)|z|2=z2;
③方程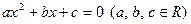 有兩個不同實數(shù)根的條件是
有兩個不同實數(shù)根的條件是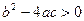 可以類比
可以類比 得到:方程
得到:方程 有兩個不同復(fù)數(shù)根的條件是
有兩個不同復(fù)數(shù)根的條件是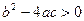 ;
;
④由向量加法的幾何意義可以類比得到復(fù)數(shù)加法的幾何意義.
其中類比錯誤的是 ( )
| A.①③ | B.②④ | C.①④ | D.②③ |
一、選擇題(本大題共8小題,每小題5分,共40分)
1.B 2. C 3. D 4.C 5.B 6.D 7.A 8. B.
二、填空題(本大題共6小題,每小題5分,共30分)
9.2009年普通高考測試題.files/image176.gif) ; 10.(-1,2); 11.0; 12.
; 10.(-1,2); 11.0; 12.2009年普通高考測試題.files/image178.gif) (或
(或2009年普通高考測試題.files/image180.gif) );
);
2009年普通高考測試題.files/image189.gif) 13.(1)
13.(1)2009年普通高考測試題.files/image191.gif) 或
或 2009年普通高考測試題.files/image193.gif) ;(2)16;(3)
;(2)16;(3)2009年普通高考測試題.files/image195.gif) .
.
三、解答題(本大題共6小題,共80分)
14.(本小題滿分12分)
解:(Ⅰ)∵2009年普通高考測試題.files/image115.gif)
2009年普通高考測試題.files/image198.gif)
當2009年普通高考測試題.files/image117.gif) 時,其圖象如右圖所示.---4分
時,其圖象如右圖所示.---4分
(Ⅱ)函數(shù)的最小正周期是2009年普通高考測試題.files/image201.gif) ,其單調(diào)遞增區(qū)間是
,其單調(diào)遞增區(qū)間是2009年普通高考測試題.files/image203.gif) ;由圖象可以看出,當
;由圖象可以看出,當2009年普通高考測試題.files/image205.gif) 時,該函數(shù)的最大值是
時,該函數(shù)的最大值是2009年普通高考測試題.files/image207.gif) .--------------7分
.--------------7分
(Ⅲ)若x是△ABC的一個內(nèi)角,則有2009年普通高考測試題.files/image209.gif) ,∴
,∴2009年普通高考測試題.files/image211.gif)
由2009年普通高考測試題.files/image119.gif) ,得
,得2009年普通高考測試題.files/image214.gif)
∴2009年普通高考測試題.files/image216.gif) ∴
∴2009年普通高考測試題.files/image218.gif) ,
,2009年普通高考測試題.files/image220.gif) ,故△ABC為直角三角形. --------------12分
,故△ABC為直角三角形. --------------12分
15.(本小題滿分12分)
解:(Ⅰ)2009年普通高考測試題.files/image222.gif)
2009年普通高考測試題.files/image224.gif) --------6分
--------6分
(Ⅱ)當2009年普通高考測試題.files/image135.gif) 時,
時,2009年普通高考測試題.files/image227.gif)
2009年普通高考測試題.files/image229.gif) ----------12分
----------12分
16.(本小題滿分14分)
2009年普通高考測試題.files/image230.gif) 解:(Ⅰ)該幾何體的直觀圖如圖1所示,它是有一條
解:(Ⅰ)該幾何體的直觀圖如圖1所示,它是有一條
側(cè)棱垂直于底面的四棱錐. 其中底面ABCD是邊長為6的
正方形,高為CC1=6,故所求體積是
2009年普通高考測試題.files/image232.gif) ------------------------4分
------------------------4分
2009年普通高考測試題.files/image233.gif) (Ⅱ)依題意,正方體的體積是原四棱錐體積的3倍,
(Ⅱ)依題意,正方體的體積是原四棱錐體積的3倍,
故用3個這樣的四棱錐可以拼成一個棱長為6的正方體,
其拼法如圖2所示. ------------------------6分
證明:∵面ABCD、面ABB
正方形,于是
2009年普通高考測試題.files/image235.gif) 故所拼圖形成立.---8分
故所拼圖形成立.---8分
2009年普通高考測試題.files/image236.gif) (Ⅲ)方法一:設(shè)B1E,BC的延長線交于點G,
(Ⅲ)方法一:設(shè)B1E,BC的延長線交于點G,
連結(jié)GA,在底面ABC內(nèi)作BH⊥AG,垂足為H,
連結(jié)HB1,則B1H⊥AG,故∠B1HB為平面AB1E與
平面ABC所成二面角或其補角的平面角. --------10分
在Rt△ABG中,2009年普通高考測試題.files/image238.gif) ,則
,則
2009年普通高考測試題.files/image240.gif) ,
,2009年普通高考測試題.files/image242.gif) ,
,
2009年普通高考測試題.files/image244.gif) ,故平面AB1E與平面ABC所成二面角的余弦值為
,故平面AB1E與平面ABC所成二面角的余弦值為2009年普通高考測試題.files/image246.gif) .---14分
.---14分
方法二:以C為原點,CD、CB、CC1所在直線分別為x、y、z軸建立直角坐標系(如圖3),∵正方體棱長為6,則E(0,0,3),B1(0,6,6),A(6,6,0).
設(shè)向量n=(x,y,z),滿足n⊥2009年普通高考測試題.files/image248.gif) ,n⊥
,n⊥2009年普通高考測試題.files/image250.gif) ,
,
于是2009年普通高考測試題.files/image252.gif) ,解得
,解得2009年普通高考測試題.files/image254.gif) .
--------------------12分
.
--------------------12分
取z=2,得n=(2,-1,2). 又2009年普通高考測試題.files/image256.gif) (0,0,6),
(0,0,6),2009年普通高考測試題.files/image258.gif)
故平面AB1E與平面ABC所成二面角的余弦值為2009年普通高考測試題.files/image246.gif) .
----------------14分
.
----------------14分
17.(本小題滿分14分)
解:分別記該考生考上第1、2、3批分數(shù)線為事件A、B、C,被相應(yīng)志愿錄取為事件Ai、Bi、Ci,(i=a、b), 則以上各事件相互獨立. -------------------------------------2分
(Ⅰ)“該考生被第2批b志愿錄取”包括上第1批分數(shù)線和僅上第2批分數(shù)線兩種情況,故所求概率為
2009年普通高考測試題.files/image260.gif)
2009年普通高考測試題.files/image262.gif)
2009年普通高考測試題.files/image264.gif) . -----------------------------------------------------------------------------------6分
. -----------------------------------------------------------------------------------6分
(Ⅱ)設(shè)該考生所報志愿均未錄取的概率為2009年普通高考測試題.files/image266.gif) ,則
,則
2009年普通高考測試題.files/image268.gif)
2009年普通高考測試題.files/image270.gif)
2009年普通高考測試題.files/image272.gif)
2009年普通高考測試題.files/image274.gif)
2009年普通高考測試題.files/image276.gif)
2009年普通高考測試題.files/image278.gif)
2009年普通高考測試題.files/image280.gif) .
.
∴該考生能被錄取的概率為2009年普通高考測試題.files/image282.gif) . ------------10分
. ------------10分
|