
題目列表(包括答案和解析)
雙曲線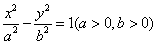 的左、右焦點分別為
的左、右焦點分別為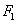 、
、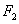 ,離心率為
,離心率為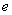 ,過
,過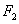 的直線與雙曲線的右支交于
的直線與雙曲線的右支交于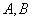 兩點,若
兩點,若 是以
是以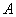 為直角頂點的等腰直角三角形,則
為直角頂點的等腰直角三角形,則
(A)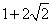 (B)
(B)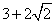 (C)
(C)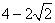 (D)
(D)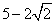
雙曲線 的左、右焦點分別為
的左、右焦點分別為 和
和 ,左、右頂點分別為
,左、右頂點分別為 和
和 ,過焦點
,過焦點 與
與 軸垂直的直線和雙曲線的一個交點為
軸垂直的直線和雙曲線的一個交點為 ,若
,若 是
是 和
和 的等比中項,則該雙曲線的離心率為
.
的等比中項,則該雙曲線的離心率為
.
雙曲線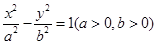 的左、右焦點分別為
的左、右焦點分別為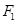 和
和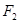 ,左、右頂點分別為
,左、右頂點分別為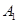 和
和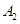 ,過焦點
,過焦點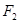 與
與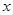 軸垂直的直線和雙曲線的一個交點為
軸垂直的直線和雙曲線的一個交點為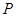 ,若
,若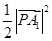 是
是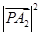 和
和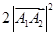 的等差中項,則該雙曲線的離心率為 .
的等差中項,則該雙曲線的離心率為 .
已知雙曲線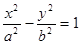 的左、右焦點分別為
的左、右焦點分別為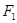 、
、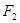 ,
, 為雙曲線的中心,
為雙曲線的中心,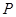 是雙曲線右支上的一點,△
是雙曲線右支上的一點,△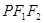 的內切圓的圓心為
的內切圓的圓心為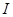 ,且⊙
,且⊙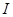 與
與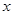 軸相切于點
軸相切于點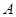 ,過
,過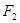 作直線
作直線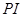 的垂線,垂足為
的垂線,垂足為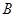 ,若
,若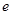 為雙曲線的離心率,則( )
為雙曲線的離心率,則( )
A.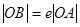 B.
B.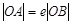
C.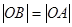 D.
D.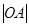 與
與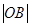 關系不確定
關系不確定
雙曲線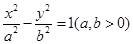 的左、右焦點分別為F1、F2,過焦點F2且垂直于x軸的直線與雙曲線相交于A、B兩點,若
的左、右焦點分別為F1、F2,過焦點F2且垂直于x軸的直線與雙曲線相交于A、B兩點,若 ,則雙曲線的離心率為
,則雙曲線的離心率為
一、選擇題(本大題共10小題,每題5分,共50分)
1.C 2.A 3.B 4.D 5.B
6.B 7.C 8.D 9.D 10.A
二、填空題(本大題共7小題,每題4分,共28分)
11.2 12.45 13. 14.
14.
15.1 16.144 17.
三、解答題(本大題共5小題,第18―20題各14分,第21、22題各15分,共72分)
18.(1)因為 (4分)
(4分)
所以
(Ⅱ)由(I)得,
 (10分)
(10分)
因為 所以
所以 ,所以
,所以 (12分)
(12分)
因此,函數 的值域為
的值域為 。(14分)
。(14分)
19.(I)因為 ,所以
,所以 平面
平面 。 (3分)
。 (3分)
又因為 平面
平面 所以
所以 ①(5分)
①(5分)
在 中,
中, ,由余弦定理,
,由余弦定理,
得
因為 ,所以
,所以 ,即
,即 。② (7分)
。② (7分)
由①,②及 ,可得
,可得 平面
平面 (8分)
(8分)
(Ⅱ)方法一;
在 中,過
中,過 作
作 于
于 ,則
,則 ,所以
,所以 平面
平面
在 中,過
中,過 作
作 于
于 ,連
,連 ,則
,則 平面
平面 ,
,
 所以
所以 為二面角
為二面角 的平面角 (11分)
的平面角 (11分)
在 中,求得
中,求得 ,
,
在 中,求得
中,求得 ,
,
所以 所以
所以 。
。
因此,所求二面角 的大小的余弦值為
的大小的余弦值為 。
。
方法二:
如圖建立空間直角坐標系 (9分)
(9分)
則

 設平面
設平面 的法向量為
的法向量為 ,
,
則
所以 ,取
,取 ,
,
則 (11分)
(11分)
又設平面 的法向量為
的法向量為 ,
,
則
 ,取
,取 ,則
,則 (13分)
(13分)
所以,
因此,所求二面角 的大小余弦值為
的大小余弦值為 。
。
20.(I) (6分)
(6分)
(Ⅱ)



1
2
3
4
5






 (14分)
(14分)
21.(I)由題意得 (3分)
(3分)
解得 (5分)
(5分)
所以橢圓方程為 (6分)
(6分)
(Ⅱ)直線 方程為
方程為 ,則
,則 的坐標為
的坐標為 (7分)
(7分)
設 則
則 ,
,
直線 方程為
方程為 令
令 ,得
,得 的橫坐標為
的橫坐標為
 ① (10分)
① (10分)
又 得
得 得
得 , (12分)
, (12分)
代入①得 , (14分)
, (14分)
得 ,
,  為常數4 (15分)
為常數4 (15分)
22.(I) (2分)
(2分)
由于 ,故嘗
,故嘗 時,
時, ,所以
,所以 , (4分)
, (4分)
故函數 在
在 上單調遞增。 (5分)
上單調遞增。 (5分)
(Ⅱ)令 ,得到
,得到 (6分)
(6分)
 的變化情況表如下: (8分)
的變化情況表如下: (8分)


0


一
0
+


極小值

因為函數 有三個零點,所以
有三個零點,所以 有三個根,
有三個根,
有因為當 時,
時, ,
,
所以 ,故
,故 (10分)
(10分)
(Ⅲ)由(Ⅱ)可知 在區間
在區間 上單調遞減,在區間
上單調遞減,在區間 上單調遞增。
上單調遞增。
所以 (11分)
(11分)


記 則
則 (僅在
(僅在 時取到等號),
時取到等號),
所以 遞增,故
遞增,故 ,
,
所以 (13分)
(13分)
于是
故對
 ,所以
,所以 (15分)
(15分)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com