
題目列表(包括答案和解析)
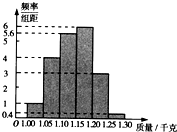 為了了解一個小水庫中養殖的魚有關情況,從這個水庫中多個不同位置捕撈出100條魚,稱得每條魚的質量(單位:千克),并將所得數據分組,畫出頻率分布直方圖(如圖所示)
為了了解一個小水庫中養殖的魚有關情況,從這個水庫中多個不同位置捕撈出100條魚,稱得每條魚的質量(單位:千克),并將所得數據分組,畫出頻率分布直方圖(如圖所示)| 分組 | 頻率 |
| [1.00,1.05) | |
| [1.05,1.10) | |
| [1.10,1.15) | |
| [1.15,1.20) | |
| [1.20,1.25) | |
| [1.25,1.30] |

| 月收入 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
| 贊成人數 | 4 | 9 | 12 | 5 | 1 | 1 |
| 非高收入族 | 高收入族 | 總計 | |
| 贊成 | |||
| 不贊成 | |||
| 總計 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 |
| k0 | 5.024 | 6.635 | 7.879 |
為了讓人們感受到丟棄塑料袋對環境造成的影響,某班環保小組的六名同學記錄了自己家中一周內丟棄的塑料袋的數量,結果如下(單位:個):33、25、28、26、25、31,如果該班有45名同學,那么根據提供的數據估計這周全班同學各家總共丟棄塑料袋的數量約為
A.900 B.1080 C.1260 D.1800
一、選擇題:本大題共12小題,每小題5分,共60分.在每小題給出的四個選項中,只有一項是符合題目要求的.
1.A 2.B 3.C 4.A 5.B
6.D 7.A 8.C 9.D 10.C
二、填空題:本大題共4小題,每小題4分,共16分.
11. 12.
12. 13.
13. 或
或 14.
14.
15. 16.
16. (也可表示成
(也可表示成 ) 17.①②③
) 17.①②③
三、解答題:本大題共6小題,共74分.
18.解:(Ⅰ)由

 ---------4分
---------4分
由 ,得
,得
即
則 ,即
,即 為鈍角,故
為鈍角,故 為銳角,且
為銳角,且
則
故 .
---------8分
.
---------8分
(Ⅱ)設 ,
,
由余弦定理得
解得
故 .
---------14分
.
---------14分
19.解:(Ⅰ)由 ,得
,得 面
面
則平面 平面
平面 ,
,
由 平面
平面 平面
平面 ,
,
則 在平面
在平面 上的射影在直線
上的射影在直線 上,
上,
又 在平面
在平面 上的射影在直線
上的射影在直線 上,
上,
則 在平面
在平面 上的射影即為點
上的射影即為點 ,
,
故 平面
平面 .
--------6分
.
--------6分
(Ⅱ)連接 ,由
,由 平面
平面 ,得
,得 即為直線
即為直線 與平面
與平面 所成角。
所成角。
在原圖中,由已知,可得
折后,由 平面
平面 ,知
,知
則 ,即
,即
則在 中,有
中,有 ,
, ,則
,則 ,
,
故
即折后直線 與平面
與平面 所成角的余弦值為
所成角的余弦值為 .
--------14分
.
--------14分
20.解:(Ⅰ)由 ,
,
得

又 ,故
,故
故數列 為等比數列;
--------6分
為等比數列;
--------6分
(Ⅱ)由(Ⅰ)可知 ,
,
則
則 對任意的
對任意的 恒成立
恒成立
由不等式 對
對 恒成立,得
恒成立,得
 .
--------14分
.
--------14分
21.解:
(Ⅰ)由已知可得
此時 ,
--------4分
,
--------4分
由 得
得 的單調遞減區間為
的單調遞減區間為 ;----7分
;----7分
(Ⅱ)由已知可得 在
在 上存在零點且在零點兩側
上存在零點且在零點兩側 值異號
值異號
⑴ 時,
時, ,不滿足條件;
,不滿足條件;
⑵ 時,可得
時,可得 在
在 上有解且
上有解且
設
①當 時,滿足
時,滿足 在
在 上有解
上有解
 或
或 此時滿足
此時滿足
②當 時,即
時,即 在
在 上有兩個不同的實根
上有兩個不同的實根
則
 無解
無解
綜上可得實數 的取值范圍為
的取值范圍為 .
--------15分
.
--------15分
22.解:(Ⅰ)(?)由已知可得 ,
,
則所求橢圓方程 . --------3分
. --------3分
(?)由已知可得動圓圓心軌跡為拋物線,且拋物線 的焦點為
的焦點為 ,準線方程為
,準線方程為 ,則動圓圓心軌跡方程為
,則動圓圓心軌跡方程為 .
--------6分
.
--------6分
(Ⅱ)由題設知直線 的斜率均存在且不為零
的斜率均存在且不為零
設直線 的斜率為
的斜率為 ,
, ,則直線
,則直線 的方程為:
的方程為:
聯立
消去 可得
可得 --------8分
--------8分
由拋物線定義可知:
 -----10分
-----10分
同理可得 --------11分
--------11分
又
(當且僅當 時取到等號)
時取到等號)
所以四邊形 面積的最小值為
面積的最小值為 .
--------15分
.
--------15分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com