
題目列表(包括答案和解析)
函數![]() 在區間
在區間![]() 上單調遞減,則
上單調遞減,則![]() 的取值范圍是
的取值范圍是
|
若函數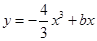 在區間
在區間 上單調遞減,則
上單調遞減,則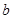 的取值范圍是( )
的取值范圍是( )
A.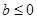 B.
B.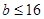 C.
C.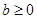 D.
D.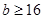
已知函數![]() 在區間
在區間![]() 上單調遞減,則
上單調遞減,則![]() 的取值范圍是
的取值范圍是
函數![]() 在區間
在區間![]() 上單調遞減,則實數
上單調遞減,則實數![]() 的取值范圍是 .
的取值范圍是 .
函數![]() 在區間
在區間![]() 上單調遞減,則實數
上單調遞減,則實數![]() 的取值范圍是( )
的取值范圍是( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
一、選擇題:本大題共12小題,每小題5分,共60分,將每小題給出的四個選項中的唯一正確的選項填在答題卡相應的題號中。
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
D
A
C
D
A
D
D
A
D
B
|