題目列表(包括答案和解析)
（本題12分）
火車站有某公司等待運送的甲種貨物1530噸，乙種貨物1150噸。現計劃用A、B兩種型號的車廂共50節運送這批貨物。已知35噸甲種貨物和15噸乙種貨物可裝滿一節A型車廂；25噸甲種貨物和35噸乙種貨物可裝滿一節B型車廂。
(Ⅰ)請你根據以上條件，安排A、B兩種型號的車廂的節數，列出所有可能的方案；
(Ⅱ)若每節A型車廂的運費是0.5萬元，每節B型車廂的運費是0.8萬元，哪種方案的運費最少？請你說明理由.
（本題12分）
火車站有某公司等待運送的甲種貨物1530噸，乙種貨物1150噸。現計劃用A、B兩種型號的車廂共50節運送這批貨物。已知35噸甲種貨物和15噸乙種貨物可裝滿一節A型車廂；25噸甲種貨物和35噸乙種貨物可裝滿一節B型車廂。
(Ⅰ)請你根據以上條件，安排A、B兩種型號的車廂的節數，列出所有可能的方案；
(Ⅱ)若每節A型車廂的運費是0.5萬元，每節B型車廂的運費是0.8萬元，哪種方案的運費最少？請你說明理由.
（本小題滿分12分）已知A、B、C三個箱子中各裝有2個完全相同的球，每個箱子里的球，有一個球標著號碼1，另一個球標著號碼2．現從A、B、C三個箱子中各摸出1個球．
（Ⅰ）若用數組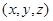
中的
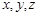分別表示從A、B、C三個箱子中摸出的球的號碼，請寫出數組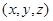的所有情形，并回答一共有多少種；
（Ⅱ）如果請您猜測摸出的這三個球的號碼之和，猜中有獎．那么猜什么數獲獎的可能性最大？請說明理由。
（本小題滿分12分）有A、B、C、D、E五位工人參加技能競賽培訓．現分別從A、B二人在培訓期間參加的若干次預賽成績中隨機抽取8次．用莖葉圖表示這兩組數據如下：
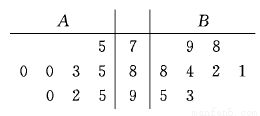
(1)現要從A、B中選派一人參加技能競賽，從平均狀況和方差的角度考慮，你認為派哪位工人參加合適?請說明理由；
(2)若從參加培訓的5位工人中選2人參加技能競賽，求A、B二人中至少有一人參加技能競賽的概率．
一、選擇題（本大題共12小題，每題5分，共60分）
1．A 2．B 3．C 4．A 5．D 6．C 7．B 8．C 9．A
10．B 11．（理）C（文）B 12．D
二、填空題（本大題共4小題，每題4分，共16分）
13．
14．②③ 15．47 16．□
三、解答題（本大題共6小題，共計76分）
17．解：
（1）依題意函數
的圖象按向量
平移后得
………………………2分
即=
………………………4分
又
比較得a=1，b=0 ………………………6分
（2）
=
………………………9分
∴
的單調增區間為[
，
]
……………………12分
18．解：
（1）設連對的個數為y，得分為x
因為y=0，1，2，4，所以x=0，2，4，8.
|
……………………6分
………………………12分
19．解法一：以D為原點，DA，DC，DD1
……………………………………2分
⊥面ADD1A1
=0，∴
⊥
，又∵MN
面ADD1A1，∴MN∥面ADD1A1；………4分
，又
=（4，1，2），又你ABCD的一個法向量為
=（0，0，1）
………………………8分
為平面DEN的法向量
⊥
，
），
），
（
所以面DEN的一個法向量
……………………12分
∴PF∥DD1，PF⊥面ABCD
，AE=
，
……………………12分
）
……………………2分
，
）
（
……………………7分
為[1，4]上單調減函數，
在[1，4]上恒成立，所以不等式
在[1，4]上恒成立。
在,[1，4]上恒成立 ……………………10分
=
在[1，4]上為減函數
……………………12分
在[0，1]上單調遞增，在區間
上單調遞
a=4 ………………………4分
的圖象與函數
恰有3個不等實根，
有兩個非零不等實根
……………………12分
①…………………2分
②
……………………5分
…………………6分
…………………8分
……………………10分
……………………12分
①…………………2分
，所以
…………………5分
與橢圓交于A（x1，y1），B（x2，y2），N點所在直線方
，由
得
……………………6分
………………8分
,所以四邊形OANB為平行四邊形 …………………9分
……………………11分
），由
，
……………………14分