
題目列表(包括答案和解析)
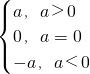 ,可以證明,對任意a,b∈R,不等式|a|-|b|≤|a+b|≤|a|+|b|成立.
,可以證明,對任意a,b∈R,不等式|a|-|b|≤|a+b|≤|a|+|b|成立.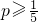 ,求|A∩B|的取值范圍.
,求|A∩B|的取值范圍.
|
| 1 |
| 5 |
|
| 1 |
| 5 |
一.選擇題
CADAD CBCAD BB
二.填空題
 ;61; 4;
;61; 4; 
三.解答題
17. 解:(I)由 得
得 …………………………….2分
…………………………….2分
即 ,所以
,所以 為第一、三象限角
為第一、三象限角
又 即
即 ,所以
,所以 ,故
,故 ……………..4分
……………..4分
(II)原式 …………………………………6分
…………………………………6分
 ……..10分
……..10分
18.解: ……………..2分
……………..2分
 ……………..4分
……………..4分
 ,且該區間關于
,且該區間關于 對稱的. ……………..6分
對稱的. ……………..6分
又 恰好有3個元素,所以
恰好有3個元素,所以 .
……………..8分
.
……………..8分
即 ,
……………..10分
,
……………..10分
解之得: . ……………..12分
. ……………..12分
19. 解:(Ⅰ)∵ 
 , ……………..2分
, ……………..2分
∴  ,
,
∴ 的圖象的對稱中心為
的圖象的對稱中心為 ,
……………..4分
,
……………..4分
又已知點 為
為 的圖象的一個對稱中心,∴
的圖象的一個對稱中心,∴ ,
,
而 ,∴
,∴ 或
或 .
……………..6分
.
……………..6分
(Ⅱ)若 成立,即
成立,即 時,
時, ,
, ,…8分
,…8分
由 ,
……………..10分
,
……………..10分
∵  是
是 的充分條件,∴
的充分條件,∴ ,解得
,解得 ,
,
即 的取值范圍是
的取值范圍是 .
……………..12分
.
……………..12分
20.(1) 1分
1分
又當 時,
時, 2分
2分
當 時,
時,
上式對 也成立,
也成立,
∴ ,
,
總之, 5分
5分
(2)將不等式變形并把 代入得:
代入得:
 7分
7分
設
∴
∴
又∵
∴ ,即
,即 . 10分
. 10分
∴ 隨
隨 的增大而增大,
的增大而增大, ,
,
∴ . 12分
. 12分
21. 解:(I)
 即
即
即 ………………………………………………..2分
………………………………………………..2分
由正弦定理得:
整理得: ………………………………………..4分
………………………………………..4分
由余弦定理得:
又 …………………………………………………………………………6分
…………………………………………………………………………6分
(II)由 ,即
,即
又 ……..8分
……..8分
另一方面 …………………...10分
…………………...10分
由余弦定理得
當且僅當 時取等號,所以
時取等號,所以 的最小值為
的最小值為 ……………………………………………12分
……………………………………………12分
22. 解:(I)由題意知 .
.
又對 ,
,
 ,即
,即 在
在 上恒成立,
上恒成立, 在
在 上恒成立。所以
上恒成立。所以 即
即 .………………………..........3分
.………………………..........3分
 ,于是
,于是
由 得
得 或
或 ,所以
,所以 的遞增區間為
的遞增區間為 ………………….4分
………………….4分
(II) .
.
 。又
。又 在
在 上是增函數,
上是增函數,
所以原不等式
 .
.
設 ,只需
,只需 的最小值不小于
的最小值不小于 .………………………....6分
.………………………....6分
又 .
.
所以,當 時取等號,即
時取等號,即 ,
,
解得 .
.
又 所以只需
所以只需 .
.
所以存在這樣的 值使得不等式成立.………………………………………………………...8分
值使得不等式成立.………………………………………………………...8分
(III)由 變形得
變形得
 ,
,
令 ,
,
要使對任意的 ,恒有
,恒有 成立,
成立,
只需滿足 ,……………………………………...10分
,……………………………………...10分
解得 ,即
,即 .……………………………………………………...12分
.……………………………………………………...12分
備選題:
設全集 ,函數
,函數 的定義域為A,集合
的定義域為A,集合 ,若
,若 恰好有2個元素,求a的取值集合.
恰好有2個元素,求a的取值集合.

18.(本小題滿分12分)
已知函數 .
.
(Ⅰ)當 時,若
時,若 ,求函數
,求函數 的值;
的值;
(Ⅱ)把函數 的圖象按向量
的圖象按向量 平移得到函數
平移得到函數 的圖象,若函數
的圖象,若函數 是偶函數,寫出
是偶函數,寫出 最小的向量
最小的向量 的坐標.
的坐標.
解:(Ⅰ) ,
,


 .
.
(Ⅱ)設 ,所以
,所以 ,要使
,要使 是偶函數,
是偶函數,
即要 ,即
,即 ,
,
 ,
,
當 時,
時, 最小,此時
最小,此時 ,
, , 即向量
, 即向量 的坐標為
的坐標為
22.(本小題滿分14分)
已知數列 有
有 ,
, (常數
(常數 ),對任意的正整數
),對任意的正整數 ,
, ,并有
,并有 滿足
滿足 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)試確定數列 是否是等差數列,若是,求出其通項公式,若不是,說明理由;
是否是等差數列,若是,求出其通項公式,若不是,說明理由;
(Ⅲ)對于數列 ,假如存在一個常數
,假如存在一個常數 使得對任意的正整數
使得對任意的正整數 都有
都有 ,且
,且 ,則稱
,則稱 為數列
為數列 的“上漸近值”,令
的“上漸近值”,令 ,求數列
,求數列 的“上漸近值”.
的“上漸近值”.
解:(Ⅰ) ,即
,即
(Ⅱ)


∴ 是一個以
是一個以 為首項,
為首項, 為公差的等差數列。
為公差的等差數列。
(Ⅲ)


∴

又∵ ,∴數列
,∴數列 的“上漸近值”為
的“上漸近值”為 。
。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com