
題目列表(包括答案和解析)
三菱柱ABC-A1B1C1中,底面邊長和側棱長都相等, BAA1=CAA1=60°
則異面直線AB1與BC1所成角的余弦值為____________.
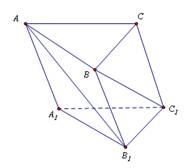
【解析】如圖設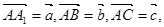 設棱長為1,則
設棱長為1,則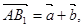
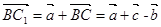 ,因為底面邊長和側棱長都相等,且
,因為底面邊長和側棱長都相等,且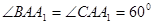 所以
所以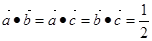 ,所以
,所以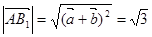 ,
,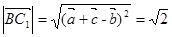 ,
,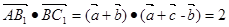 ,設異面直線的夾角為
,設異面直線的夾角為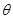 ,所以
,所以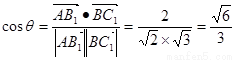 .
.
設函數f(x)= 在[1,+∞
在[1,+∞ 上為增函數.
上為增函數.
(1)求正實數a的取值范圍;
(2)比較 的大小,說明理由;
的大小,說明理由;
(3)求證: (n∈N*, n≥2)
(n∈N*, n≥2)
【解析】第一問中,利用
解:(1)由已知: ,依題意得:
,依題意得: ≥0對x∈[1,+∞
≥0對x∈[1,+∞ 恒成立
恒成立
∴ax-1≥0對x∈[1,+∞ 恒成立 ∴a-1≥0即:a≥1
恒成立 ∴a-1≥0即:a≥1
(2)∵a=1 ∴由(1)知:f(x)= 在[1,+∞)上為增函數,
在[1,+∞)上為增函數,
∴n≥2時:f( )=
)=
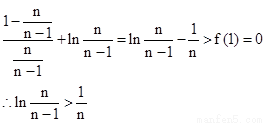
(3) ∵ ∴
∴
已知 .
.
(1)求 的單調區間;
的單調區間;
(2)證明:當 時,
時, 恒成立;
恒成立;
(3)任取兩個不相等的正數 ,且
,且 ,若存在
,若存在 使
使 成立,證明:
成立,證明: .
.
【解析】(1)g(x)=lnx+ ,
, =
=
 (1’)
(1’)
當k 0時,
0時, >0,所以函數g(x)的增區間為(0,+
>0,所以函數g(x)的增區間為(0,+ ),無減區間;
),無減區間;
當k>0時, >0,得x>k;
>0,得x>k; <0,得0<x<k∴增區間(k,+
<0,得0<x<k∴增區間(k,+ )減區間為(0,k)(3’)
)減區間為(0,k)(3’)
(2)設h(x)=xlnx-2x+e(x 1)令
1)令 = lnx-1=0得x=e, 當x變化時,h(x),
= lnx-1=0得x=e, 當x變化時,h(x), 的變化情況如表
的變化情況如表
|
x |
1 |
(1,e) |
e |
(e,+ |
|
|
|
- |
0 |
+ |
|
h(x) |
e-2 |
|
0 |
↗ |
所以h(x) 0, ∴f(x)
0, ∴f(x) 2x-e
(5’)
2x-e
(5’)
設G(x)=lnx- (x
(x 1)
1)  =
= =
=
 0,當且僅當x=1時,
0,當且僅當x=1時, =0所以G(x) 為減函數, 所以G(x)
=0所以G(x) 為減函數, 所以G(x)  G(1)=0, 所以lnx-
G(1)=0, 所以lnx-
 0所以xlnx
0所以xlnx
 (x
(x 1)成立,所以f(x)
1)成立,所以f(x) 
 ,綜上,當x
,綜上,當x 1時, 2x-e
1時, 2x-e f(x)
f(x)
 恒成立.
恒成立.
(3) ∵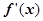 =lnx+1∴lnx0+1=
=lnx+1∴lnx0+1= =
= ∴lnx0=
∴lnx0=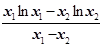 -1
∴lnx0 –lnx
-1
∴lnx0 –lnx =
= -1–lnx
-1–lnx =
= =
= =
= (10’) 設H(t)=lnt+1-t(0<t<1),
(10’) 設H(t)=lnt+1-t(0<t<1),
 =
= =
=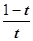 >0(0<t<1), 所以H(t) 在(0,1)上是增函數,并且H(t)在t=1處有意義, 所以H(t)
<H(1)=0∵
>0(0<t<1), 所以H(t) 在(0,1)上是增函數,并且H(t)在t=1處有意義, 所以H(t)
<H(1)=0∵ ∴
∴ =
=
∴lnx0 –lnx >0, ∴x0 >x
>0, ∴x0 >x
如圖,已知四棱錐 的底面ABCD為正方形,
的底面ABCD為正方形,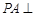 平面ABCD,E、F分別是BC,PC的中點,
平面ABCD,E、F分別是BC,PC的中點, ,
, .
.
(1)求證: 平面
平面 ;
;
(2)求二面角 的大小.
的大小.

【解析】第一問利用線面垂直的判定定理和建立空間直角坐標系得到法向量來表示二面角的。

第二問中,以A為原點,如圖所示建立直角坐標系
 ,,
,,
設平面FAE法向量為 ,則
,則
 ,
, ,
,

【練】
(1)(2005全國卷1)已知橢圓的中心為坐標原點O,焦點在![]() 軸上,斜率為1且過橢圓右焦點F的直線交橢圓于A、B兩點,
軸上,斜率為1且過橢圓右焦點F的直線交橢圓于A、B兩點,![]() 與
與![]() 共線。(Ⅰ)求橢圓的離心率;(Ⅱ)設M為橢圓上任意一點,且
共線。(Ⅰ)求橢圓的離心率;(Ⅱ)設M為橢圓上任意一點,且![]() ,證明
,證明![]() 為定值。
為定值。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com