題目列表(包括答案和解析)
（本小題滿分12分）在一個不透明的盒子中，放有標號分別為1，2，3的三個大小相同的小球，現從這個盒子中，有放回地先后取得兩個小球，其標號分別為
，記
． （1）求隨機變量
的最大值，并求事件“取得最大值”的概率；
（2）求隨機變量的分布列和數學期望．
（本小題滿分12分）在我校值周活動中，甲、乙等五名值周生被隨機地分到A，B，C，D四個不同的崗位服務，每個崗位至少有一名值周生．
(1)求甲、乙兩人同時參加A崗位服務的概率；
(2)求甲、乙兩人不在同一個崗位服務的概率；
(3)設隨機變量X為這五名值周生中參加A崗位服務的人數，求X的分布列及期望．
（本小題滿分12分）
在一次體操選拔賽中，教練組設置了難度不同的甲、乙兩個系列，每個系列都有A和B兩個動作．比賽時每位運動員自選一個系列完成，兩個動作得分之和為該運動員的成績．
假設每個運動員完成每個系列中的兩個動作的得分是相互獨立的．根據賽前訓練統計數據，某運動員完成甲系列和乙系列的情況如下表：
表1：甲系列 表2：乙系列
|
|
現該運動員最后一個出場，之前其他運動員的最高得分為115分．
（Ⅰ）若該運動員希望獲得該項目的第一名，應選擇哪個系列？說明理由，并求其獲得第一名的概率；
（Ⅱ）若該運動員選擇乙系列，求其成績
的分布列及其數學期望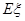
．
（本小題滿分12分）
在平面直角坐標系xOy中，經過點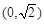
且斜率為k的直線l與橢圓
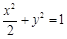有兩個不同的交點P和Q.
（Ⅰ）求k的取值范圍；
（Ⅱ）設橢圓與x軸正半軸、y軸正半軸的交點分別為A、B，是否存在常數k，使得向量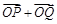
與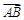
共線？如果存在，求k值；如果不存在，請說明理由.
（本小題滿分12分）
在
這
個自然數中，任取
個不同的數．
（1）求這個數中至少有
個是偶數的概率；
（2）設
為這個數中兩數相鄰的組數（例如：若取出的數為
，則有兩組相鄰的數1，2和2，3，此時的值是
）．求隨機變量的分布列及其數學期望
。
1．B 2．B 3．A 4．C 5．C 6．B 7．D 8．B 9．C 10．B
11．A 12．D
【解析】
1．，所以選B．
2．的系數是，所以選B．
3．，所以選．
4．為鈍角或，所以選C
5．，所以選C．
6．，所以選B．
7．，所以選D．
8．化為或，所以選B．
9．將左移個單位得，所以選A．
10．直線與橢圓有公共點，所以選B．
11．如圖，設，則，
,
,從而，因此與底面所成角的正弦值等于．所以選A．
12．畫可行域 可知符合條件的點是：共6個點，故，所以選D．
二、
13．185．．
14．60．．
15．，由，得
．
16．．如圖：
如圖，可設，又，
．
當面積最大時，．點到直線的距離為．
三、
17．（1）由三角函數的定義知：．
（2）
．
18．（1）設兩年后出口額恰好達到危機前出口額的事件為，則．
（2）設兩年后出口額超過危機前出口額的事件為，則．
19．（1）設與交于點．
從而，即，又，且
平面為正三角形，為的中點，
，且，因此，平面．
（2）平面，∴平面平面又，∴平面平面
設為的中點，連接，則，
平面，過點作，連接，則．
為二面角的平面角．
在中，．
又．
20．（1）
（2）
又
綜上：．
21．（1）的解集為（1，3）
∴1和3是的兩根且
由此得
時，時，
在處取得極小值
③
由式①、②、③聯立得：
．
（2）
∴當時，在上單調遞減，
當時，
當時，在[2，3]上單調遞增，
22．（1）由得
∴橢圓的方程為：．
（2）由得，
又
設直線的方程為：
由得
由此得． ①
設與橢圓的交點為，則
由得
，整理得
，整理得
時，上式不成立， ②
由式①、②得
或
∴取值范圍是．
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
