
題目列表(包括答案和解析)
對于數列![]() ,如果存在一個正整數
,如果存在一個正整數![]() ,使得對任意的
,使得對任意的![]() (
(![]() )都有
)都有![]() 成立,那么就把這樣一類數列
成立,那么就把這樣一類數列![]() 稱作周期為
稱作周期為![]() 的周期數列,
的周期數列,![]() 的最小值稱作數列
的最小值稱作數列![]() 的最小正周期,以下簡稱周期。例如當
的最小正周期,以下簡稱周期。例如當![]() 時
時![]() 是周期為
是周期為![]() 的周期數列,當
的周期數列,當![]() 時
時![]() 是周期為
是周期為![]() 的周期數列。
的周期數列。
(1)設數列![]() 滿足
滿足![]() (
(![]() ),
),![]() (
(![]() 不同時為0),且數列
不同時為0),且數列![]() 是周期為
是周期為![]() 的周期數列,求常數
的周期數列,求常數![]() 的值;
的值;
(2)設數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() .
.
①若![]() ,試判斷數列
,試判斷數列![]() 是否為周期數列,并說明理由;
是否為周期數列,并說明理由;
②若![]() ,試判斷數列
,試判斷數列![]() 是否為周期數列,并說明理由;
是否為周期數列,并說明理由;
(3)設數列![]() 滿足
滿足![]() (
(![]() ),
),![]() ,
,![]() ,
,![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,試問是否存在
,試問是否存在![]() ,使對任意的
,使對任意的![]() 都有
都有![]() 成立,若存在,求出
成立,若存在,求出![]() 的取值范圍;不存在, 說明理由;
的取值范圍;不存在, 說明理由;
| π |
| 2 |
| Sn |
| n |
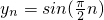 時,{yn}的周期為4的周期數列.
時,{yn}的周期為4的周期數列.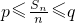 成立,若存在,求出p、q的取值范圍;不存在,說明理由.
成立,若存在,求出p、q的取值范圍;不存在,說明理由.| π |
| 2 |
| Sn |
| n |
 時,{yn}的周期為4的周期數列.
時,{yn}的周期為4的周期數列. 成立,若存在,求出p、q的取值范圍;不存在,說明理由.
成立,若存在,求出p、q的取值范圍;不存在,說明理由.一、選擇題:(本大題12個小題,每小題5分,共60分)
CDAB,DABC,CBDA
二、填空題:(本大題4個小題,每小題4分,共16分)
13.0; 14.3; 15.3; 16.10
三、解答題:(本大題6個小題,共74分)
17.(12分)
解:(Ⅰ)由已知等式得: …………(2分)
…………(2分)
 ………………(5分)
………………(5分)
 ………………………………………………………………(6分)
………………………………………………………………(6分)
(Ⅱ) ……………………………………(8分)
……………………………………(8分)
 ……………………(11分)
……………………(11分)
 ………………………………………………………………(12分)
………………………………………………………………(12分)
18.(12分)
解:由
 ………………………………(2分)
………………………………(2分)
①當 時,
時, ;……………………………(6分)
;……………………………(6分)
②當 時,
時, ;…………………………………………(8分)
;…………………………………………(8分)
③當 時,
時, 。………………………………(11分)
。………………………………(11分)
綜上,當 時,
時, ;
;
當 時,
時, ;
;
當 時,
時, 。………………………(12分)
。………………………(12分)
19.(12分)
解:(Ⅰ)
 ………………………………(7分)
………………………………(7分)
(Ⅱ)
 ………………………(12分)
………………………(12分)
20.(12分)
解:設商場分配給超市部、服裝部、家電部的營業額依次為 萬元,
萬元, 萬元,
萬元, 萬元(
萬元( 均為正整數),由題意得:
均為正整數),由題意得:
 ………………………………(5分)
………………………………(5分)
由(1),(2)得 ………………………………(7分)
………………………………(7分)
 ………………………………(8分)
………………………………(8分)

 ………………………………(9分)
………………………………(9分)
 ………………(11分)
………………(11分)
答:分配給超市部、服裝部、家電部的營業額分別為12萬元,22萬元,21萬元,售貨員人數分別為48人,110人,42人;或者分配給三部門的營業額依次為15萬元,20萬元,20萬元,售貨員人數分別為60人,100人,40人。……………………(12分)
21.(12分)
解:(Ⅰ)設拋物線頂點為 ,則拋物線的焦點為
,則拋物線的焦點為 ,由拋物線的定義可得:
,由拋物線的定義可得:
 ……………………………(6分)
……………………………(6分)
(Ⅱ)不存在。…………………………………………………………(7分)
設過點 ,斜率為
,斜率為 的直線方程為
的直線方程為 (斜率不存在時,顯然不合題意),………………………………………………………………………………(8分)
(斜率不存在時,顯然不合題意),………………………………………………………………………………(8分)
由 …………………………(9分)
…………………………(9分)
由 ………………………………………………………(10分)
………………………………………………………(10分)
假設在軌跡 上存在兩點
上存在兩點 ,令
,令 的斜率分別為
的斜率分別為 ,則
,則
顯然不可能滿足
∴軌跡 上不存在滿足
上不存在滿足 的兩點。………………………………(12分)
的兩點。………………………………(12分)
22.(14分)
(Ⅰ)解:由 ,可以化為:
,可以化為:
 ………………………………(1分)
………………………………(1分)
從而 …………………………………………………………(3分)
…………………………………………………………(3分)
又由已知 ,得:
,得:
 , 即
, 即 
∴數列 是首項為
是首項為 ,公差為
,公差為 的等差數列,…………………………(4分)
的等差數列,…………………………(4分)
 ……………………(8分)
……………………(8分)
(Ⅱ)證明: ……(9分)
……(9分)
 (12分)
(12分)
(Ⅲ)解:由于 ,若
,若 恒成立
恒成立
 ………………………………(14分)
………………………………(14分)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com