
題目列表(包括答案和解析)
設橢圓 的左、右頂點分別為
的左、右頂點分別為 ,點
,點 在橢圓上且異于
在橢圓上且異于 兩點,
兩點, 為坐標原點.
為坐標原點.
(Ⅰ)若直線 與
與 的斜率之積為
的斜率之積為 ,求橢圓的離心率;
,求橢圓的離心率;
(Ⅱ)若 ,證明直線
,證明直線 的斜率
的斜率
 滿足
滿足
【解析】(1)解:設點P的坐標為 .由題意,有
.由題意,有 ①
①
由 ,得
,得 ,
,
由 ,可得
,可得 ,代入①并整理得
,代入①并整理得
由于 ,故
,故 .于是
.于是 ,所以橢圓的離心率
,所以橢圓的離心率
(2)證明:(方法一)
依題意,直線OP的方程為 ,設點P的坐標為
,設點P的坐標為 .
.
由條件得 消去
消去 并整理得
并整理得 ②
②
由 ,
, 及
及 ,
,
得 .
.
整理得 .而
.而 ,于是
,于是 ,代入②,
,代入②,
整理得
由 ,故
,故 ,因此
,因此 .
.
所以 .
.
(方法二)
依題意,直線OP的方程為 ,設點P的坐標為
,設點P的坐標為 .
.
由P在橢圓上,有
因為 ,
, ,所以
,所以 ,即
,即 ③
③
由 ,
, ,得
,得 整理得
整理得 .
.
于是 ,代入③,
,代入③,
整理得
解得 ,
,
所以 .
.
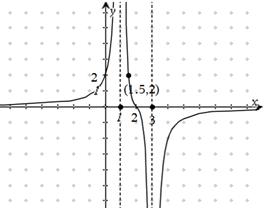
已知函數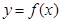 的圖像(如圖所示)過點
的圖像(如圖所示)過點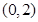 、
、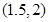 和點
和點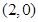 ,且函數圖像關于點
,且函數圖像關于點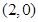 對稱;直線
對稱;直線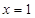 和
和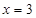 及
及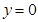 是它的漸近線.現要求根據給出的函數圖像研究函數
是它的漸近線.現要求根據給出的函數圖像研究函數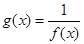 的相關性質與圖像,
的相關性質與圖像,
(1)寫出函數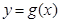 的定義域、值域及單調遞增區間;
的定義域、值域及單調遞增區間;
(2)作函數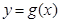 的大致圖像(要充分反映由圖像及條件給出的信息);
的大致圖像(要充分反映由圖像及條件給出的信息);
(3)試寫出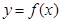 的一個解析式,并簡述選擇這個式子的理由(按給出理由的完整性及表達式的合理、簡潔程度分層給分
的一個解析式,并簡述選擇這個式子的理由(按給出理由的完整性及表達式的合理、簡潔程度分層給分
下列推理:
①由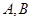 為兩個不同的定點,動點
為兩個不同的定點,動點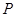 滿足
滿足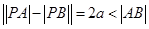 ,得點
,得點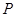 的軌跡為雙曲線
的軌跡為雙曲線
②由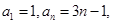 ,求出
,求出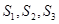 猜想出數列
猜想出數列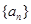 的前
的前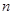 項和
項和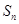 的表達式
的表達式
③由圓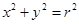 的面積
的面積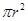 ,猜想出橢圓
,猜想出橢圓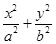 =1的面積
=1的面積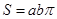
④科學家利用魚的沉浮原理制造潛艇。其中是歸納推理的命題個數為 ( )
| A.0 | B.1 | C.2 | D.3 |
下列推理:
①由![]() 為兩個不同的定點,動點
為兩個不同的定點,動點![]() 滿足
滿足![]() ,得點
,得點![]() 的軌跡為雙曲線
的軌跡為雙曲線
②由![]() ,求出
,求出![]() 猜想出數列
猜想出數列![]() 的前
的前![]() 項和
項和![]() 的表達式
的表達式
③由圓![]() 的面積
的面積![]() ,猜想出橢圓
,猜想出橢圓![]() =1的面積
=1的面積![]()
④科學家利用魚的沉浮原理制造潛艇。其中是歸納推理的命題個數為 ( )
A.0 B.1 C.2 D.3
| y+1 |
| x-1 |
| x2+y2 |
| (x-1)2+y2 |
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com