
題目列表(包括答案和解析)
 、
、 是平面內(nèi)一組基向量,且
是平面內(nèi)一組基向量,且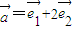 、
、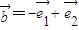 ,則向量
,則向量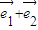 可以表示為另一組基向量
可以表示為另一組基向量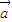 、
、 的線性組合,即
的線性組合,即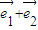 =
= 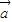 +
+ 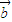 .
.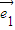 、
、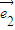 是平面內(nèi)一組基向量,且
是平面內(nèi)一組基向量,且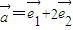 、
、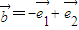 ,則向量
,則向量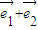 可以表示為另一組基向量
可以表示為另一組基向量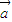 、
、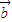 的線性組合,即
的線性組合,即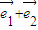 =
= 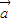 +
+ 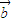 .
.設(shè)![]() 、
、![]() 是平面內(nèi)一組基向量,且
是平面內(nèi)一組基向量,且![]() 、
、![]() ,則向量
,則向量![]() 可以表示為另一組基向量
可以表示為另一組基向量![]() 、
、![]() 的線性組合,即
的線性組合,即![]()
![]()
![]() .
.
設(shè)![]() 、
、![]() 是平面內(nèi)一組基向量,且
是平面內(nèi)一組基向量,且![]() 、
、![]() ,則向量
,則向量![]() 可以表示為另一組基向量
可以表示為另一組基向量![]() 、
、![]() 的線性組合,即
的線性組合,即![]()
![]()
![]() .
.
A. |
B. |
C. |
D. |
一、填空題(每題5分,理科總分55分、文科總分60分):
1. 2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image261.gif) ; 2.
理:2;文:
; 2.
理:2;文:2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image263.gif) ; 3. 理:1.885;文:2;
; 3. 理:1.885;文:2;
4. 理:2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image265.gif) ;文:1.885; 5. 理:
;文:1.885; 5. 理:2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image267.gif) ;文:4; 6. 理:
;文:4; 6. 理:2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image269.gif) ;文:
;文:2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image265.gif) ;
;
7. 理:2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image271.gif) ;文:
;文:2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image267.gif) ; 8. 理:
; 8. 理:2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image273.gif) ;文:6; 9. 理:
;文:6; 9. 理:2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image275.gif) ;文:
;文:2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image277.gif) ;
;
10. 理:1; 文:2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image273.gif) ; 11. 理:
; 11. 理:2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image279.gif) ;文:
;文:2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image275.gif) ; 12. 文:
; 12. 文:2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image279.gif) ;
;
二、選擇題(每題4分,總分16分):
題號
理12;文13
理13;文14
理:14;文:15
理15;文:16
答案
A
C
B
C
三、解答題:
16.(理,滿分12分)
解:因為拋物線的焦點2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image228.gif) 的坐標(biāo)為
的坐標(biāo)為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image282.gif) ,設(shè)
,設(shè)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image284.gif) 、
、2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image286.gif) ,
,
由條件,則直線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image243.gif) 的方程為
的方程為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image289.gif) ,
,
代入拋物線方程2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image291.gif) ,可得
,可得2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image293.gif) ,則
,則2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image295.gif) .
.
于是,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image297.gif) .
.
…2
…4
…8
…12
17.(文,滿分12分)
解:因為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image299.gif) ,所以由條件可得
,所以由條件可得2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image301.gif) ,
,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image095.gif) .
.
即數(shù)列2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image152.gif) 是公比
是公比2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image304.gif) 的等比數(shù)列.
的等比數(shù)列.
又2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image306.gif) ,
,
所以,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image308.gif) .
.
…4
…6
…8
…12
(理)17.(文)18. (滿分14分)
解:因為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image310.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image312.gif)
所以,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image314.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image316.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image318.gif)
即2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image320.gif) 或
或2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image322.gif) ,
,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image324.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image326.gif) 或
或2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image328.gif) ,
,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image324.gif)
又由2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image175.gif) ,即
,即
當(dāng)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image330.gif) 時,
時,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image332.gif) 或
或2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image334.gif) ;當(dāng)
;當(dāng)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image336.gif) 時,
時,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image338.gif) 或
或2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image340.gif) .
.
所以,集合2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image342.gif) .
.
…3
…7
…11
…14
18.(理,滿分15分,第1小題6分,第2小題9分)
解:(1)當(dāng)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image344.gif) 時,
時,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image346.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image348.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image350.gif)
故2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image352.gif) ,
,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image354.gif) ,所以
,所以2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image356.gif) .
.
(2)證:由數(shù)學(xué)歸納法
(i)當(dāng)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image358.gif) 時,易知
時,易知2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image360.gif) ,為奇數(shù);
,為奇數(shù);
(ii)假設(shè)當(dāng)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image362.gif) 時,
時,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image364.gif) ,其中
,其中2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image366.gif) 為奇數(shù);
為奇數(shù);
則當(dāng)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image368.gif) 時,
時,
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image370.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image372.gif)
所以2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image374.gif) ,又
,又2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image376.gif) 、
、2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image378.gif) ,所以
,所以2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image380.gif) 是偶數(shù),
是偶數(shù),
而由歸納假設(shè)知2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image366.gif) 是奇數(shù),故
是奇數(shù),故2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image383.gif) 也是奇數(shù).
也是奇數(shù).
綜上(i)、(ii)可知,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image385.gif) 的值一定是奇數(shù).
的值一定是奇數(shù).
證法二:因為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image387.gif)
當(dāng)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image389.gif) 為奇數(shù)時,
為奇數(shù)時,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image391.gif)
則當(dāng)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image358.gif) 時,
時,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image360.gif) 是奇數(shù);當(dāng)
是奇數(shù);當(dāng)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image395.gif) 時,
時,
因為其中2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image397.gif) 中必能被2整除,所以為偶數(shù),
中必能被2整除,所以為偶數(shù),
于是,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image391.gif) 必為奇數(shù);
必為奇數(shù);
當(dāng)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image389.gif) 為偶數(shù)時,
為偶數(shù)時,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image400.gif)
其中2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image402.gif) 均能被2整除,于是
均能被2整除,于是2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image385.gif) 必為奇數(shù).
必為奇數(shù).
綜上可知,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image091.gif) 各項均為奇數(shù).
各項均為奇數(shù).
…3
…6
…8
…10
…14
…15
…10
…14
…15
19. (文,滿分14分)
解:如圖,設(shè)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image406.gif) 中點為
中點為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image408.gif) ,聯(lián)結(jié)
,聯(lián)結(jié)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image410.gif) 、
、2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image412.gif) .
.
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image413.gif) 由題意,
由題意,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image415.gif) ,
,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image189.gif) ,所以
,所以2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image417.gif) 為等邊三角形,
為等邊三角形,
故2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image419.gif) ,且
,且2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image421.gif) .
.
又2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image423.gif) ,
,
所以2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image425.gif) .
.
而圓錐體的底面圓面積為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image427.gif) ,
,
所以圓錐體體積2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image429.gif) .
.
…3
…8
…10
…14
(理)19. (文)20. (滿分16分,第1小題4分,第2小題6分,第3小題6分)
解:(1)由題意,當(dāng)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image207.gif) 和
和2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image209.gif) 之間的距離為
之間的距離為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image207.gif) 應(yīng)位于
應(yīng)位于2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image432.gif) 上方,
上方,
且此時2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image205.gif) 中
中2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image207.gif) 邊上的高為
邊上的高為
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image436.gif) 又因為
又因為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image438.gif) 米,可得
米,可得2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image440.gif) 米.
米.
所以,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image442.gif) 平方米,
平方米,
即三角通風(fēng)窗2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image213.gif) 的通風(fēng)面積為
的通風(fēng)面積為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image445.gif) 平方米.
平方米.
(2)12008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image447.gif) 如圖(1)所示,當(dāng)
如圖(1)所示,當(dāng)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image207.gif) 在矩形區(qū)域滑動,即
在矩形區(qū)域滑動,即2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image449.gif) 時,
時,
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image451.gif) 的面積
的面積2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image453.gif) ;
;
22008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image447.gif) 如圖(2)所示,當(dāng)
如圖(2)所示,當(dāng)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image207.gif) 在半圓形區(qū)域滑動,即
在半圓形區(qū)域滑動,即2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image455.gif) 時,
時,
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image456.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image458.gif) ,故可得
,故可得2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image451.gif) 的面積
的面積
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image460.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image462.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image464.gif) ;
;
綜合可得:
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image466.gif)
(3)12008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image447.gif) 當(dāng)
當(dāng)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image207.gif) 在矩形區(qū)域滑動時,
在矩形區(qū)域滑動時,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image014.gif) 在區(qū)間
在區(qū)間2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image469.gif) 上單調(diào)遞減,
上單調(diào)遞減,
則有2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image471.gif) ;
;
22008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image447.gif) 當(dāng)
當(dāng)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image207.gif) 在半圓形區(qū)域滑動時,
在半圓形區(qū)域滑動時,
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image473.gif) ,
,
等號成立2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image475.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image477.gif) ,
,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image455.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image475.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image480.gif) .
.
因而當(dāng)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image482.gif) (米)時,每個三角通風(fēng)窗
(米)時,每個三角通風(fēng)窗2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image213.gif) 得到最大通風(fēng)面積,最大面積為
得到最大通風(fēng)面積,最大面積為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image485.gif) (平方米).
(平方米).
…2
…4
…6
…9
…10
…12
…15
…16
21(文,滿分18分,第1小題5分,第2小題6分,第3小題7分)
解:(1)設(shè)右焦點坐標(biāo)為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image487.gif) (
(2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image489.gif) ).
).
因為雙曲線C為等軸雙曲線,所以其漸近線必為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image491.gif) ,
,
由對稱性可知,右焦點2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image228.gif) 到兩條漸近線距離相等,且
到兩條漸近線距離相等,且2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image494.gif) .
.
于是可知,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image496.gif) 為等腰直角三角形,則由
為等腰直角三角形,則由2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image236.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image498.gif) ,
,
又由等軸雙曲線中,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image500.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image502.gif) .
.
即,等軸雙曲線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image238.gif) 的方程為
的方程為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image505.gif) .
.
(2)設(shè)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image284.gif) 、
、2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image286.gif) 為雙曲線
為雙曲線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image238.gif) 直線
直線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image243.gif) 的兩個交點.
的兩個交點.
因為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image511.gif) ,直線
,直線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image243.gif) 的方向向量為
的方向向量為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image241.gif) ,直線
,直線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image243.gif) 的方程為
的方程為
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image513.gif) .
.
代入雙曲線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image238.gif) 的方程
的方程2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image505.gif) ,可得
,可得2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image515.gif) ,
,
于是有2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image517.gif)
而2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image519.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image521.gif) .
.
(3)假設(shè)存在定點2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image523.gif) ,使
,使2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image258.gif) 為常數(shù),其中
為常數(shù),其中2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image525.gif) ,
,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image527.gif) 為直線
為直線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image243.gif) 與雙曲線
與雙曲線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image238.gif) 的兩個交點的坐標(biāo).
的兩個交點的坐標(biāo).
①當(dāng)直線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image243.gif) 與
與2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image053.gif) 軸不垂直時,設(shè)直線
軸不垂直時,設(shè)直線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image243.gif) 的方程為
的方程為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image534.gif)
代入2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image505.gif) ,可得
,可得2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image536.gif) .
.
由題意可知,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image538.gif) ,則有
,則有2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image540.gif) ,
,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image542.gif) .
.
于是,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image544.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image546.gif)
2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image548.gif)
要使2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image258.gif) 是與
是與2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image550.gif) 無關(guān)的常數(shù),當(dāng)且僅當(dāng)
無關(guān)的常數(shù),當(dāng)且僅當(dāng)2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image552.gif) ,此時
,此時2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image554.gif) .
.
②當(dāng)直線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image243.gif) 與
與2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image053.gif) 軸垂直時,可得點
軸垂直時,可得點2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image557.gif) ,
,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image559.gif) ,
,
若2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image552.gif) ,
,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image554.gif) 亦為常數(shù).
亦為常數(shù).
綜上可知,在2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image053.gif) 軸上存在定點
軸上存在定點2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image561.gif) ,使
,使2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image554.gif) 為常數(shù).
為常數(shù).
…3
…5
…7
…9
…11
…13
…16
…17
…18
20(理,滿分22分,第1小題4分,第2小題6分,第3小題12分)
解:(1)解法一:由題意,四邊形2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image193.gif) 是直角梯形,且
是直角梯形,且2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image410.gif) ∥
∥2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image406.gif) ,
,
則2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image566.gif) 與
與2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image410.gif) 所成的角即為
所成的角即為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image569.gif) .
.
因為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image571.gif) ,又
,又2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image573.gif) 平面
平面2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image193.gif) ,
,
所以2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image576.gif) 平面
平面2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image578.gif) ,則有
,則有2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image580.gif) .
.
因為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image582.gif) ,
,2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image419.gif) ,
,
所以2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image585.gif) ,則
,則2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image587.gif) ,
,
即異面直線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image566.gif) 與
與2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image410.gif) 所成角的大小為
所成角的大小為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image589.gif) .
.
解法二:如圖,以2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image246.gif) 為原點,直線
為原點,直線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image209.gif) 為
為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image053.gif) 軸、直線
軸、直線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image410.gif) 為
為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image055.gif) 軸、直線
軸、直線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image596.gif) 為
為2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image598.gif) 軸,
軸,
建立空間直角坐標(biāo)系.
于是有2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image600.gif) 、
、2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image602.gif) ,則有
,則有2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image604.gif) ,又
,又2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image606.gif)
則異面直線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image566.gif) 與
與2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image410.gif) 所成角
所成角2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image608.gif) 滿足
滿足2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image610.gif) ,
,
所以,異面直線2008學(xué)年度第二學(xué)期高三年級質(zhì)量調(diào)研數(shù)學(xué)試題(文科)2009.04.files/image566.gif) 與
與
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com