為了在夏季降溫和冬季供暖時減少能源損耗，房屋的屋頂和外墻需要建造隔熱層。某幢建筑物要建造可使用20年的隔熱層，每厘米厚的隔熱層建造成本為6萬元。該建筑物每年的能源消耗費用C（單位：萬元）與隔熱層厚度x（單位：cm）滿足關系：C（x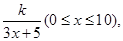）=若不建隔熱層（即x=0時），每年能源消耗費用為8萬元.設f（x）為隔熱層建造費用與20年的能源消耗費用之和.

（1）求k的值；

（2）求f(x)的表達式；

（3）利用“函數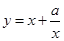（其中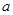為大于0的常數），在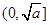上是減函數，在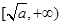上是增函數”這一性質，求隔熱層修建多厚時，總費用f(x)達到最小，并求出這個最小值.

為了在夏季降溫和冬季供暖時減少能源損耗，房屋的屋頂和外墻需要建造隔熱層。某幢建筑物要建造可使用20年的隔熱層，每厘米厚的隔熱層建造成本為6萬元。該建筑物每年的能源消耗費用C（單位：萬元）與隔熱層厚度x（單位：cm）滿足關系：C（x）=若不建隔熱層（即x=0時），每年能源消耗費用為8萬元.設f（x）為隔熱層建造費用與20年的能源消耗費用之和.
（1）求k的值；
（2）求f(x)的表達式；
（3）利用“函數（其中為大于0的常數），在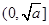上是減函數，在上是增函數”這一性質，求隔熱層修建多厚時，總費用f(x)達到最小，并求出這個最小值.

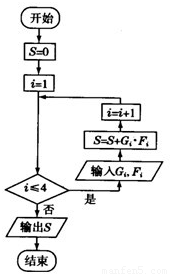
為了讓學生更多的了解“數學史”知識，某中學高一年級舉辦了一次“追尋先哲的足跡，傾聽數學的聲音”的數學史知識競賽活動，共有800名學生參加了這次競賽．為了解本次競賽的成績情況，從中抽取了部分學生的成績（得分均為整數，滿分為100分）進行統計．請你根據頻率分布表，解答下列問題：

序號 （i）	分組 （分數）	組中值（Gi）	頻數 （人數）	頻率（Fi）
1	[60，70）	65	①	0.16
2	[70，80）	75	22	②
3	[80，90）	85	14	0.28
4	[90，100]	95	③	④
合　　計			50	1

（1）填充頻率分布表中的空格（在解答中直接寫出對應空格序號的答案）；
（2）為鼓勵更多的學生了解“數學史”知識，成績不低于80分的同學能獲獎，那么可以估計在參加的800名學生中大概有多少同學獲獎？
（3）在上述統計數據的分析中有一項計算見算法流程圖，求輸出S的值．