日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

（本題滿分12分）

設函數，，是的一個極大值點．

   （Ⅰ）若，求的取值范圍；

   （Ⅱ） 當是給定的實常數，設是的3個極值點，問是否存在實數，可找到，使得的某種排列（其中=）依次成等差數列?若存在，求所有的及相應的；若不存在，說明理由．

（本題滿分12分）

設函數，，是的一個極大值點．

   （Ⅰ）若，求的取值范圍；

   （Ⅱ） 當是給定的實常數，設是的3個極值點，問是否存在實數，可找到，使得的某種排列（其中=）依次成等差數列?若存在，求所有的及相應的；若不存在，說明理由．

（本題滿分12分）
設二次函數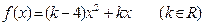，對任意實數，有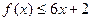恒成立；數列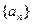滿足.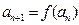
（1）求函數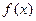的解析式；
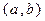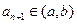（2）試寫出一個區間，使得當時，且數列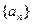是遞增數列，并說明理由；
（3）已知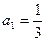，是否存在非零整數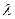，使得對任意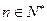，都有
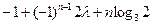 恒成立，若存在，求之；若不存在，說明理由.

（本題滿分12分） 設函數（），．

(1) 將函數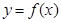圖象向右平移一個單位即可得到函數的圖象，試寫出的解析式及值域；

(2) 關于的不等式的解集中的整數恰有3個，求實數的取值范圍；

(3) 對于函數與定義域上的任意實數，若存在常數，使得和都成立，則稱直線為函數與的“分界線”．設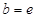，，試探究與是否存在“分界線”？若存在，求出“分界線”的方程；若不存在，請說明理由．

（本題滿分12分）

設二次函數，對任意實數，有恒成立；數列滿足.

（1）求函數的解析式；

（2）試寫出一個區間，使得當時，且數列是遞增數列，并說明理由；

（3）已知，是否存在非零整數，使得對任意，都有

 恒成立，若存在，求之；若不存在，說明理由.