日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

查看答案和解析>>

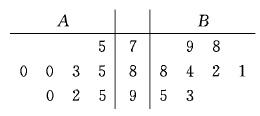
（本小題滿分12分）有A、B、C、D、E五位工人參加技能競賽培訓．現分別從A、B二人在培訓期間參加的若干次預賽成績中隨機抽取8次．用莖葉圖表示這兩組數據如下：

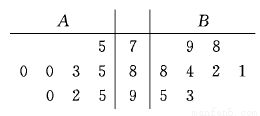
(1)現要從A、B中選派一人參加技能競賽，從平均狀況和方差的角度考慮，你認為派哪位工人參加合適?請說明理由；
(2)若從參加培訓的5位工人中選2人參加技能競賽，求A、B二人中至少有一人參加技能競賽的概率．

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

一、選擇題（每小題5分，共12小題）

    BADAC    ABBCB    CD

二、填空題（每小題4分，共4小題）

13．0

14．n+(n+1)+…+(3n－2)=(2n－1)²

15．256+64π

16．①③

三、解答題

   （I）∵(2a－c)cosB=bcosC，

∴（2sinA－sinC）cosB=sinBcosC.……………………………………………2分

即2sinAcosB=sinBcosC+sinCcosB

=sin(B+C)

∵A+B+C=π，∴2sinAcosB=sinA.…………………………………………4分

∵0<A<π,∴sinA≠0.

∴cosB=.…………………………………………………………………5分

∵0<B<π，∴B=.…………………………………………………………6分

  （II）=4ksinA+cos2A.…………………………………………………………7分

=－2sin²A+4ksinA+1，A∈（0，）……………………………………9分

設sinA=t，則t∈.

則=－2t²+4kt+1=－2(t－k)²+1+2k²,t∈.…………………………10分

∵k>1，∴t=1時，取最大值.

依題意得，－2+4k+1=5，∴k=.………………………………………………12分

（18）（I）證明：

          連接B₁C，與BC₁相交于O，連接OD

          ∵BCC₁B₁是矩形，

∴O是B₁C的中點.

又D是AC的中點，

∴OD//AB₁.………………………………………………2分

∵AB_­1面BDC_­1，OD面BDC₁，

∴AB₁//面BDC₁.…………………………………………4分

   （II）解：如力，建立空間直角坐標系，則

         C₁（0，0，0），B（0，3，2），C（0，3，0），A（2，3，0），

         D（1，3，0）……………………5分

即.…………6分

易知=(0，3，0)是面ABC的一個法向量.

.…………………………8分

∴二面角C₁―BD―C的余弦值為.………………………………9分

   （III）假設側棱AA₁上存在一點P（2，y，0）（0≤y≤3），使得CP⊥面BDC₁.

         則

          ∴方程組無解.

∴假設不成立.……………………………………………………11分

∴側棱AA₁上不存在點P，使CP⊥面BDC₁.…………………12分

19．（I）解：設答對題的個數為y，得分為ξ,y=0，1，2，4

           ∴ξ=0，2，4，8…………………………………………………………1分

           ……………………………………………………3分

           …………………………………………5分

           …………………………………………7分

           ………………………………………………9分

          則ξ的分布列為

ξ

0

2

4

8

P

   （II）Eξ=0×+2×+4×+8×=2

        答：該人得分的期望為2分………………………………12分

20．解：

   （I）由題意，令y=0，x<0，得f(x)[1－f(0)]=0，∵x<0時，f(x)>1.

        ∴1－f(0)=0. f(0)=1.…………………………………………………………2分

        適合題意的f(x)的一個解析式為f(x)=()^x.………………………………4分

   （II）①由遞推關系知f(a_n+1)?f(－2－a_n)=1，即f(a_n+1－2－a_n)=f(0).

         ∵f(x)的R上單調，∴a_n+1－a_n=2，（n∈N^*），…………………………6分

         又a₁=1，故a_n=2n－1.……………………………………………………7分

         ②b_n=,S_n=b₁+b₂+…+b_n=+()³+…+()^2n－1

         欲比較S_n與的大小，只需比較4ⁿ與2n+1的大小.

         由=1，2，3代入可知4ⁿ>2n+1，猜想4ⁿ>2n+1.……………………10分

         下用數學歸納法證明

        （i）當n=1時，4¹>2×1+1成立

        （ii）假設當n=k時命題成立，即4^k>2k+1

當n=k+1時，4^k+1=4×4^k>4(2k+1)=8k+4=2(k+1)+1+6k+1>2(k+1)+1，

說明當n=k+1時命題也成立.

由（i）（ii）可知，4ⁿ>2n+1 對于n∈N^*都成立.

故S_n>.………………………………………………………………12分

注：證明4ⁿ>2n+1，除用數學歸納法證明以外，還可用其它方法證明，

如：4ⁿ=(1+3)ⁿ=1+

21．解：（I）定圓B的圓心坐標B（－，0），半徑r=6，

因為動圓P與定圓B內切，所以|PA|+|PB|=6.

所以動圓圓心P的軌跡是以B、A為焦點，長軸長為6的橢圓.

設橢圓的方程為

則2a=6，a=3，c=

∴b²=a²－c²=4.

∴橢圓的方程為.……………………4分

   （II）設M(x₁，y₁)，N（x₂，y₂），

則由

（1）當λ=1時，M與N重合，，滿足條件。

（2）當.

     綜合可得λ的取值范圍是[，5].………………………………12分

22．解：

   （I）f′(x)=3ax²+2bx－3，依題意，f′(1)=f′(－1)=0，

        即…………………………………………2分

        解得a=1，b=0.

        ∴f(x)=x³－3x.……………………………………………………4分

   （II）∵f(x)=x³－3x,∴f′(x)=3x²－3=3(x+1)(x－1)，

當－1<x<1時，f′(x)<0，故f(x)在區間[－1，1]上為減函數，

f_max(x)=f(－1)=2，f_min(x)=f(1)=－2……………………………………6分

∵對于區間[－1，1]上任意兩個自變量的值x₁，x₂，

都有|f(x₁)－f(x₂)|≤|f_max(x) －f_min(x)|

|f(x₁)－f(x₂)|≤|f_max(x)－f_min(x)|=2－(－2)=4………………………………8分

   （III）f′(x)=3x²－3=3(x+1)(x－1)，

         ∵曲線方程為y=x³－3x，∴點A（1，m）不在曲線上.

設切點為M（x₀，y₀），則點M的坐標滿足

因，故切線的斜率為

，

整理得.

∵過點A（1，m）可作曲線的三條切線，

∴關于x₀方程=0有三個實根.……………………10分

設g(x­₀)= ，則g′(x₀)=6，

由g′(x₀)=0，得x₀=0或x₀­=1.

∴g(x₀)在（－∞，0），（1，+∞）上單調遞增，在（0，1）上單調遞減.

∴函數g(x₀)= 的極值點為x₀=0，x₀=1………………12分

∴關于x₀方程=0有三個實根的充要條件是

，解得－3<m<－2.

故所求的實數a的取值范圍是－3<m<－2.……………………14分